不整合メッシュモデルによる大規模接触解析へのアプローチ
下薗征史 博士(工学) インテスジャパン株式会社 代表取締役
1.はじめに
輸送機器に用いられるエンジン、トランスミッション、ブレーキなど複数のパーツから構成されるアセンブリモデルの設計では、パーツ間に生じる接触情報(接触状況や接触圧力など)の詳細かつ厳密な評価が重要となることが多い。例えば、合わせ面における接触圧が不均一に分布し、ガス・液漏れの原因となることや、ギア歯の不完全な当たりにより、過剰に応力が集中し歯折れに至るなど、接触状態はアセンブリパーツとしての強度や耐久性に大きく影響し、理想的な接触状態を保てないアセンブリパーツは、製品の不具合や特定部位の欠損につながる危険性も高くなる。
アセンブリモデルの接触は、パーツ間のわずかな隙間に生じる現象であり、接触圧や接触状況の分布情報を実測にて得ることは困難であるため、有限要素法をベースとした数値シミュレーションにより、接触現象を解析的に調べることが一般的に行われる。
なお、接触計算を高い精度で行うため、接触近傍部の領域を詳細要素で分割し、連続した領域には連続した要素を用いる必要がある。仮に自動要素分割機能を用いて要素寸法を段階的に変化させ、接触近傍部の詳細要素から接触遠隔部の粗大要素へ変化させることが可能でも、総節点数が増えることから、接触モデルの規模は非接触モデルに比べ大きくなる。さらに、アセンブリパーツは、複数かつ複雑な接触の機構を数多く有すことから、接触解析のための計算モデルおよび計算負荷は必然的に大規模にならざるを得ない。
本稿では、このような複数のパーツを含む大規模なアセンブリモデルに対する接触問題の計算を、精度を損なうことなく、現実的な時間で解くことができる計算モデル、ならびに計算手法の確立を主な目的としている。接触計算で得られた結果の精度検証は、ヘルツの接触理論に基づく数値との比較により行った。
本稿で提案するモデリング手法、ならびに接触モデルを積極的に活用することで、これまで敬遠していた大規模な接触計算問題を、高精度かつ短時間に行えるものと思われる。
2.不整合要素モデル

図-1 ギア歯に対する不整合要素結合
(1) 整合要素と不整合要素
一般に、有限要素解析において高い精度の計算を実現するためには、連続領域に連続要素を用い、応力集中が予想される領域については、応力や変位の分布をスムースに表現できるよう詳細な要素を用いる。ここでは、連続要素のみで構成されるモデルのことを整合要素モデルとよぶ。整合要素モデルでは、隣り合う要素間で節点を完全に共有し合う。
一方、本稿で主な検討対象とする不整合要素モデルは、連続領域に不連続要素を用い、結合境界面にて接し合う不連続な要素間で節点は非共有であり、節点に生じる変位や力は一般に使用される多点拘束方程式で表されるタイ結合(のり付け)に従い伝達される。本手法を用いることで、たとえ異なる要素タイプ同士であっても、結合境界面が判定値の許容範囲内にあれば結合可能となる[1]。しかしながら、不整合要素の結合は、結合面を境界として、ひずみや応力の連続性が失われるため、応力集中が予想される領域付近での使用は極力避け、接触領域から十分離れた分布に影響しない位置に結合境界を設定すべきである。図-1に不整合要素結合モデルの実用例を示す。
(2) 不整合要素モデルを用いる理由
不整合要素モデルの使用に際しては、応力がスムースに分布するよう、結合境界の位置を接触領域から離す必要があるものの、分布に与える影響を意識した要素分割を心掛けることで、接触解析を目的とした自由度の高いアセンブリモデルの構築が可能となる。
接触解析を精度良く行うためには、接触圧力の分布状況を的確に表現するための詳細な要素分割が必要になる。したがって、不整合要素を用いた結合を積極的に行うことで、接触近傍部には詳細な要素を集中的に配置し、離れた領域には粗大な要素を配置できるため、モデル規模が極端に増大する心配がない。アセンブリパーツの設計において、一部の領域に対する形状変更のみを集中的に行い、全体構造と変更領域を完全に切り離せることから、要素分割を初期段階からやり直す手間が解消され、その結果、開発工数の大幅な削減が期待できる。
3.接触解析のための不整合要素モデル
(1) ヘルツの接触理論
本稿では、計算結果の精度検証のため、図-2 に示したヘルツの接触理論より導出される諸式により確認を行った。本理論式は、2つのボールに対する接触を仮定しており、ここでは、片方のボールのみ曲率半径を無限大として、ボールとブロックの接触問題として考えた。
また、本稿ではあくまでも、要素分割手法と計算精度および計算コストの関係に主眼を置いたため、ボールとブロックに与える材料特性は線形弾性材料、摩擦係数をゼロと仮定したシンプルな接触問題として検討した。
(2) 接触解析のための整合要素モデル
図-3に、接触解析のための整合要素モデルを示す。使用する要素は8節点ヘキサ要素であり、計算負荷の軽減のため、荷重と構造の対称性を考慮して、ボールとブロックには対称境界条件を与えた。ボールに与える圧縮荷重は、多点拘束法に基づく荷重方向の自由度に対するリンク結合を設定し、ボール断面上の全節点で力を受けるように設定した。
(3) 接触解析のための不整合要素モデル
次に、接触解析のための不整合要素モデル例を図-4に示す。不整合要素の結合境界の存在が計算結果に与える影響を調べるため、結合境界を1つおよび2つ設定した計算モデルを用意し、理論値との比較を行った。
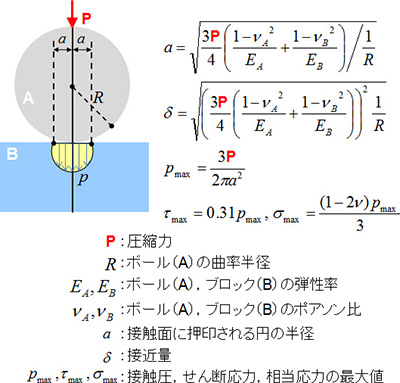
図-2 ボールとブロックに対するヘルツの接触理論

図-3接触解析のための整合要素モデル
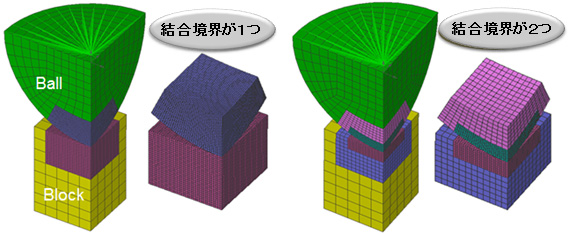
図-4接触解析のための不整合要素モデル
4.計算精度の確認
(1) 整合要素モデルによる精度検証
本稿では、まず、接触計算に用いる有限要素解析ソルバーの精度検証ならびに計算時間の確認のため、表-1に示すヘルツの接触理論から求まる理論値を用い、表-2の接触解析モデルより得られる計算結果の比較を行った。表-3に理論値との絶対誤差を、図-4に相当応力の分布状況をそれぞれ示す。
(2) 不整合要素モデルによる精度検証
次に、表-2に示す不整合要素モデルを用いた接触計算を行い、不整合要素に存在する不連続な結合境界が、計算精度に与える影響を確認した。表-3と図-4に得られた解析結果を示す。
なお、m0, m1, m2 の3モデルの接触領域における要素寸法は完全に一致しており、不整合要素の結合の違いによる精度比較ができるよう配慮した。
| 項目 | ボール | ブロック | |
| 入力条件 | 弾性率 | 200,000 MPa | 100,000 MPa |
| ポアソン比 | 0.3 | 0.3 | |
| 幾何形状 | 半径:1.0 mm | 高さ:1.0 mm | |
| 圧縮荷重 | 100 N | ||
| 出力結果 | 接触円半径 | 0.10079 mm | |
| 接近量 | 0.010158 mm | ||
| 最大接触圧 | 4700.5 MPa | ||
| 最大せん断応力 | 1457.2 MPa | ||
| 最大引張応力 | 2914.3 MPa | ||
| モデル名称 | m0 | m1 | m2 | m3 | m4 |
| 要素モデル | 整合 | 不整合 | 不整合 | 不整合 | 不整合 |
| 結合境界の数 | なし | 1 | 2 | 2 | 2 |
| 節点の幾何形状への投影 | 完全 | 完全 | 完全 | 完全 | 不完全 |
| 節点総数 | 721,839 | 77,871 | 19,781 | 89,203 | 89,203 |
| 接触部近傍の要素辺長 | 0.0148 | 0.0148 | 0.0148 | 0.0083 | 0.0083 |
| モデル名称 | m0 | m1 | m2 | m3 | m4 |
| 計算時間 | 6 hour | 46 sec | 9 sec | 50 sec | 53 sec |
| 接触円半径 | 0.39% | 0.39% | 0.49% | 4.01% | × |
| 接近量 | 1.49% | 1.37% | 1.27% | 1.12% | 31.0% |
| 最大接触圧 | 0.17% | 0.18% | 0.34% | 0.75% | 149% |
| 最大せん断応力 | 2.32% | 2.37% | 2.68% | 1.63% | 150% |
| 最大引張応力 | 2.32% | 2.37% | 2.68% | 1.63% | 150% |
本計算に用いたマシンのスペックは、CPU: INTEL Core i7/ Memory:8GB/ HDD: 5400 rpm であった。
(3) 接触節点のCAD形状への投影
ここではさらに、接触解析において接触節点を幾何形状へ正しく投影することの重要性について確認するため、補足的な検証を行った。比較を簡単に行うため、表-2に示すm3, m4モデルを例に、要素分割は全く同じであるものの、節点が球面に完全に投影されているモデルと投影されていないモデルの違いについて検討を行った。図-6に、接触節点の幾何形状への投影に関する概念図、図-7にボールおよびブロック面上の接触応力分布状況を示す。
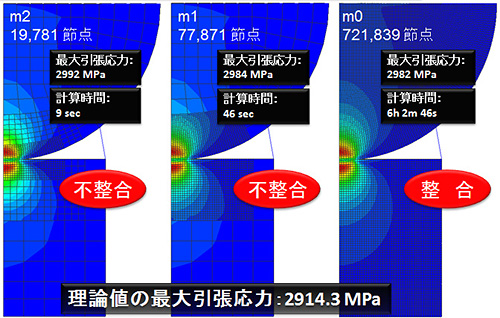
図-5引張応力分布の比較
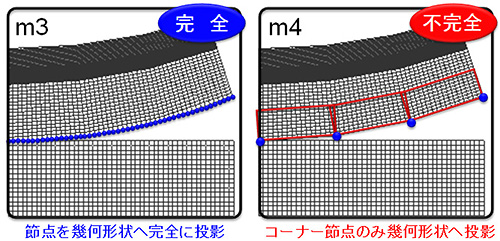
図-6節点の幾何形状への投影に関する概念図
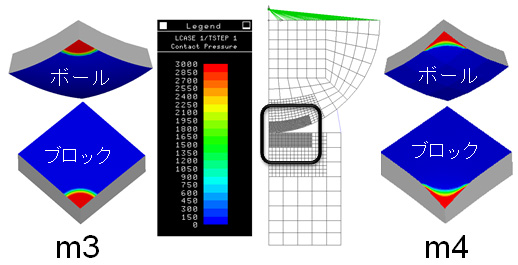
図-7ボールとブロック面上の接触応力分布状況
5.計算結果に関する考察
ここでは、本稿で提案した接触解析のためのモデリング、および解析手法について、得られた計算結果に対するそれぞれの考察を行う。
まず、整合要素モデル:m0による接触解析では、6時間を超える計算時間を必要としたことから、計算過程で生成される剛性マトリクスのサイズが大きくなり、マシンに与える負荷が高かったことが予想される。計算精度については、理論値との比較により、いずれの評価項目に対しても誤差範囲3%以内をマークしていることから、精度上特に問題がないと思われる。このことから、本稿で用いる解析ソルバーと有限要素モデルを用いれば、接触計算に関して高い精度を保てることから、不整合要素モデルを使用した接触計算についても同様の検討を行った。
不整合要素モデルの接触計算について、得られた結果より傾向分析を行う。まず、整合モデル:m0と不整合要素モデル:m1, m2, m3 の結果を比較した場合に、共通点として、計算時間が大幅に短縮され、その割に計算精度が悪化しないことが挙げられる。なお、m3の接触円半径のみ誤差が4%を超える悪い値を示しているが、接触状況と要素寸法の関係は複雑であり、必ずしも要素寸法が小さいと接触円の半径も理論値に近づくとは言い切れない。図-5に示す引張応力分布によれば、不整合要素モデルの結合境界の影響により、完全にスムースな分布は望めないものの、全体的な分布傾向をとらえることが概ね可能であることが分かる。6時間も計算時間を要して得られた整合要素モデルによる計算結果と、わずか数十秒で得られた不整合要素モデルによる計算結果との間に、精度上の差はほぼ無いと言える。
不整合要素モデルにおける結合境界の設定数の影響については、境界の数が多くなるほど、結合部での多点拘束により構造的な剛性が上がり、整合要素で得られる値と比較し離れていく傾向となるものの、計算精度を極端に損なわず、計算時間を大幅に削減できる可能性がある。本手法を積極的に用いれば、全体構造における自由度の低減が大いに期待でき、現実的な使用を想定すれば、その効果は大きい。ベアリングの接触問題[2]を例に考えても、ボールとインナーレース、ボールとアウターレース、ボールとリテーナー、これら複数の接触現象について厳密な評価を行う場合、結合境界を積極的に設定しモデルの自由度を削減する手法も有効と思われる。
また、表-3のm4の結果から、ボール表面上の節点を幾何形状に正しく投影する重要性についても確認できる。計算精度を向上するために、詳細な要素分割を行っても、分割後に新たに生成された節点を幾何形状に投影しなければ、節点数が増え計算時間が増すだけでなく、計算精度も悪化する。
表-3のm2, m3の計算結果の比較により、不整合要素モデルを用いた場合の要素寸法と計算精度の関係について定性的傾向が確認できる。要素寸法が小さくなれば、モデル規模も大きくなるので計算時間は増大するが、最大せん断応力および最大引張応力の厳密な予測を行う場合、精度向上の期待ができる。圧縮力を受けたボールの疲労欠損の発生位置などを詳細に調べる場合など、不整合要素モデルを積極的に用いることで、接触領域の要素寸法を小さくしたモデルの適用も可能になる。
6.結論
本稿では、ボールとブロックの接触問題をテーマに、不整合要素モデルを用いた数値計算による結果と、ヘルツの理論式から得られた値との詳細な比較により、以下のような知見を得た。
- 接触領域の要素寸法が同じ場合、計算精度を極端に悪化させずに、計算時間を飛躍的に短縮できる
- 段階的に不整合要素を用い、複数の結合境界が存在しても、接触領域から離れた位置で要素間を結合すれば、計算精度を大幅に損なうことなく、接触計算の高速化が図れる
- 接触面上の節点を幾何形状に正確に投影しない場合、接触計算の精度は極端に悪化し、妥当な接触現象を再現できなくなる可能性がある
- 変形体内部に発生する最大応力の値を厳密に評価する場合、不整合要素モデルを積極的に用い、できるだけ詳細な要素を使用すれば、より高い精度で疲労破壊やクラッキングの現象を予測できる
なお、本稿の接触計算のために用いた接触計算用ソルバーは、モデル全体の自由度が多い場合、計算時間もモデル規模に応じて増大するが、接触ペア数が増えて接触自由度が増した場合でも、接触計算のみを目的とするマトリクスは全体マトリクスから分離するよう取り扱えることから、接触領域に詳細要素を集中的に使用するモデルは計算コストという面では大きな問題にならない。
今後は、本稿で行ったボールとブロックの接触問題だけでなく、ギア[3]、ベアリング、ジョイント、ドライブシャフトなど、従来、モデル規模が大きく敬遠されていた大規模なアセンブリモデルの接触問題についても検討する予定である。
また、浸炭焼入れ現象に伴う焼入れ深さに応じた材料特性の変化を考慮した接触計算を行う場合、浸炭層に不整合要素モデルを適用は理想的と言える。なお、大きな圧縮力を受ける接触問題への適用についても、弾塑性材料特性や固着-すべりを含む摩擦の考慮は不可欠であり、本手法の妥当性の検証はますます必要になるものと思われる。
参考文献
[1] R. Helfrich, I. Pflieger: Simulation and Optimization of Part Connections, NAFEMS Seminar Apr 28 - 29, 2010, Wiesbaden, Germany 1996.
[2] ジェイテクト「ベアリング入門書」編集委員会: よくわかる最新ベアリングの基本と仕組み、秀和システム、2011.
[3] G. Fajdiga, M. Šraml, J. Flašker and J. Kramar: Surface fatigue of Gear Teeth Flanks, Fracture of Nano and Engineering Materials and Structures, 2006, pp 197-198.
