PERMASの自由形状最適化機能を用いた接触問題への適用
原田 裕也 インテスジャパン株式会社 テクニカル エンジニア
1.はじめに
近年、工業製品の新規開発にあたっては、世界的な環境問題に対する関心の高まりや、アジア圏をはじめとする安価な諸外国製品の台頭に対する競争力強化などを背景に、これまで以上の環境性能と、省資源・低コスト化が求められるようになった。
今日の製品開発を取り巻くこのような潮流に対して、軽量化というのがひとつのキーワードとして挙げられる。
より軽量な構造に対する探求は、航空宇宙分野などでは古くから多くの取り組みがなされてきたが、自動車などのより身近な製品においても、使用材の削減による材料コストの圧縮や、燃費の改善による環境性能の向上など、前述のニーズに寄与するため、新製品の開発において重要な課題となっている。
これらのことから、新たに開発を行う際には、従来製品を上回る品質や耐久性を達成しながら、使用環境において必要以上の強度を持つ構造とならないような効率的な形状を選定することが求められている。
このような厳しい要求に対して効率的な開発を行うにあたり、 CAEによる支援が欠かせないものとなっている。近年のハードウェア・ソフトウェア双方の進歩によって、その担う役割も大きくなっている。
2. PERMASによる最適化解析のメリット
シミュレーションによってある目的を設定し、それに対する効率的な形状を得る際に用いられるのが、最適化解析である。
最適化解析は、開発の初期段階など、各部品の形状案をおおまかに決定する場合に用いられる位相最適化と、ある程度決定された量産形状に近いものから、より効率的な詳細形状を探索する場合などに用いられる形状最適化に大別される。
本稿では、後者のうち、設計空間に含まれる表面節点を自由に移動させるノンパラメトリック形状最適化を行う。
以下に、PERMASにおける形状最適解析の主なメリットを挙げる。
2.1 接触を考慮した最適化解析
最適化解析による最適形状の探索にあたって、より現実的な形状を得るためには、単一の部品単位ではなく、アセンブリとしてその使用状況を想定した外力を考慮する必要があるため、各パーツ間における接触状況を考慮することは重要である。
PERMASでは、形状最適化を行う際に、まず接触を考慮した静解析をおこない、その結果に対して最適化解析をおこなう。そして、そこで得られた形状を用いて次の静解析を行うというプロセスを繰り返す。この際に、前回の接触解析における接触ステータスの情報をストアして利用するため、通常、初回の計算に比較して計算時間が短縮される。
2.2 構造解析と最適化解析を同一ソルバーで完結
前述のようにPERMASでは静解析と最適化解析を交互に行いながら最適解を求めていくが、このプロセスは単一のソルバー内で繰り返される。このことによるメリットして、解析結果譲渡の際のファイルへのデータ出力と、その読み込みにかかる時間を短縮できることが挙げられる。通常、最適化解析は数回から数十回の繰り返し計算を行うため、この積み重ねにより解析全体を通しての効果は高くなる。
2.3 非設計空間はマトリクス縮約し負荷を軽減
アセンブリモデルを対象とする場合、ボルトの座面やケースの合わせ面、他の部品との接続面など、形状を維持しなければならない箇所を形状変更の対象から除外する(非設計空間)。これらの非設計空間はマトリクスを縮約し、反復計算から除外することで、一回あたりの計算負荷を軽減している。
3. 解析方法とモデル概要
本稿で用いる解析モデルを図-1に示す。
車載用のオイルポンプを想定したアセンブリモデルに対し、まず構造解析を行い、その結果を用いた表面形状を設計変数としたノンパラメトリック形状最適化までを1サイクルとして行う形状変更対象のボディは全てテトラ2次要素で作成した。
3.1 接触解析モデル
構造解析における境界条件(図-2参照)と荷重パターンを以下に示す。
- STEP-1) ボディとカバー間にボルト締結力を与える。
- STEP-2) 油圧相当の圧力荷重20MPaを図-3のように与えた。
- STEP-3) 最適化計算では、ボルトの締結状態を基準とした応力制約条件を考えるため、STEP-3では、STEP-2で得られた応力分布からSTEP-1の応力分布を差し引いた差分の応力分布を新たに生成した。
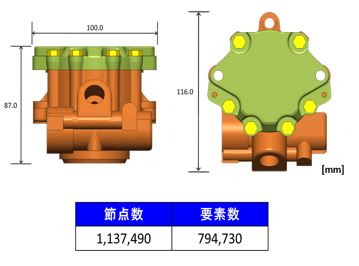
図-1 解析モデルの概要
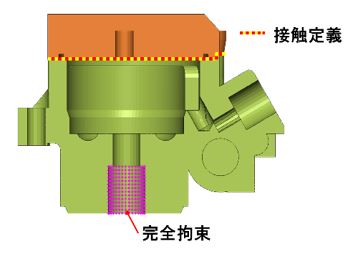
図-2 解析モデルの接触/拘束条件
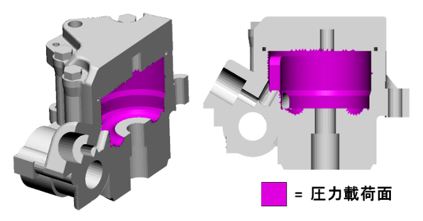
図-3 圧力載荷面
3.2 最適化解析モデル
図-4に解析モデルに用いた設計空間を示す。ボルト座面、ケースの合わせ面、および他部品との接続箇所等は設計空間から除外した。本稿では、3つの制約条件を与え、重量(最小化)を目的関数とした形状最適化を行った。
以下に最適化計算に用いた制約条件を記す。
- ・制約条件-1 : 主応力
最大主応力を絶対値で評価し、上限を90.0MPaとする。 - ・制約条件-2 : 変位
MPC(Multi Point Constraint)を2箇所作成し(図-5参照)、それぞれの制御節点に対して、初期形状の構造解析を行った際の変位量を上限値として与える。 - ・制約条件-3 : 要素品質
節点の移動を繰り返すことで、次第に要素のひずみが大きくなり、結果として解析を停止させる原因となってしまう。これに対する予防策という意味合いでPERMASが内的にもつ要素品質の評価値に対して制約を与える。

図-4 解析モデルの設計空間
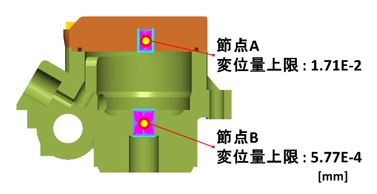
図-5 変位の設計拘束条件
4. 解析結果とその考察

図-6 肉厚変化の分布

図-7 変位分布の変化

図-8 主応力分布の変化
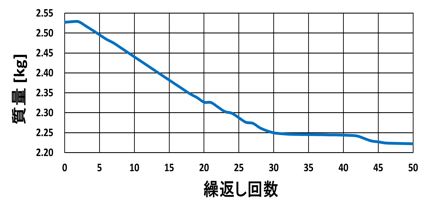
図-9 目的関数 : 質量の履歴
4.1 目的関数の履歴
初期形状に対する結果形状の肉厚変化分布を図-6に示す。ここで、赤色で表示されている箇所は薄肉方向へ変化したことを表し、モデル全体の広い範囲で肉厚が削減されたことが確認できる。次に、質量推移のグラフを図-9に示す。繰り返し回数50回以上の領域では変化が見られなかったため打ち切りとした。初期重量=2.527[kg]に対し、結果重量=2.222[kg]となり、0.305[kg]の削減で約12%の軽量化を達成した。また、計算時間は50サイクルで11時間4分となった。
4.2 制約条件の履歴
主応力最大値推移のグラフを図-10に示す。初期の最大応力値が136.82[MPa]に対して結果形状の最大値が82.58[MPa]となり、約40%の低減となった。
節点変位の推移を図-11に示す。初期の変位量に対する各イタレーションの変位量をパーセンテージで表している。節点Bではおおよそ初期の変位量を維持しているが、節点Aでは最終的に約8%の超過となった。
要素品質最大値の推移を図-12に示す。要素品質はPERMASが内部に持っている品質評価の値であり、0から1の間で表される。この値が1になると要素形状破綻により解析が停止-する。今回は0.95を上限値として設定した。初期形状では上限値をすべての要素で下回っているが、形状の更新に伴い上昇し、最終的に約2%超過した。
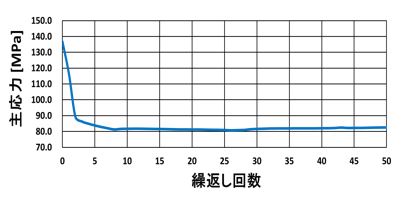
図-10 制約条件 : 主応力(絶対値)の履歴
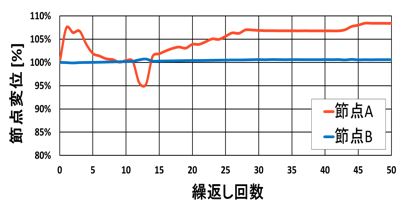
図-11 制約条件 : 節点変位の履歴
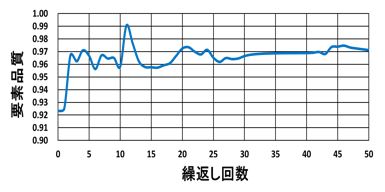
図-12 制約条件 : 要素品質の履歴
5. 結論および今後の課題
アセンブリモデルを例にPERMASを用いた接触を考慮したノンパラメトリック形状最適化を行った。目的関数である重量については約12%の削減、制約条件の応力の最大値については設定値を下回り、約40%の緩和を達成出来た。しかしながら、最適化の計算で定義した3つの制約条件のうち、応力以外の条件については、現状では制約値を超過する結果となった。この点については今後、さらに機能改善を図る必要性があるが、これらの制約が全て守られ、形状最適化が行われるようになると、ものづくりの現場において有用なシミュレーションの手法になると期待される。
現状のソフトウェアの課題として、部材の肉厚と型抜き勾配を考慮した計算が出来ないことが挙げられるが、これにより、得られた最適形状が非現実的になる可能性がある。
また、設計空間内にピン角のような直角コーナ形状が含まれていると、エッジ上の節点が初期位置から移動できず、ライン状に形状が固定され、庇のような形状に変化する(図-13参照)。これは、ノンパラメトリック形状最適化では、面の法線方向をベースに節点の移動が行われるが、直角コーナのエッジ上の節点は、異なる2つの面に属していることに起因する。そのため、これを防ぐには人為的な面取り作業を事前に行う必要がある。これらの機能追加や自動化が今後の開発課題である。
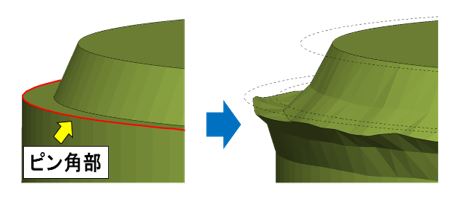
図-13 ピン角部の形状変化
