回転効果を考慮したブレーキ鳴き解析
下薗 征史 博士(工学) インテスジャパン株式会社 代表取締役
芦田 克彦 日信工業株式会社 主幹
増田 千尋 日信工業株式会社
斉藤 絵美 インテスジャパン株式会社 チーフサポートエンジニア
1.はじめに
今日のハイブリッド車に代表される内燃機関と電動機の共存に伴い、車両騒音に関する問題も少しずつ変貌を遂げようとしている。動力源の電動機へのシフトにより、従来、大きな問題であった内燃機関から生じる騒音は、ほぼ気にならないレベルになってきており、エンジン音を意識するのは、もはやアクセルを踏込み加速する場合に限るといっても過言ではない。日本国内に限れば、ブレーキが最も頻繁に使用されるのは、スタートとストップを繰返し行う、道路渋滞状況における自動車の低速走行時であるといえる。動力源に電動機を有すようになれば、低速走行状態での蓄電エネルギーによる駆動による動力源からの騒音は小さくなり、動力源が内燃機関だけだった時代に比べ、確実にシビアなブレーキ静音性能が要求されるようになるだろう。
これまでの国内車両向けのブレーキ設計におけるシミュレーション技術は、主にブレーキが低速走行状態で使用されることを前提に設計されており、ディスクローターの回転速度が低いことから、回転効果は無視してもブレーキシステム全体の振動特性に大きな影響を及ぼす可能性は低いという考えが根底にあった。
本稿では、従来のブレーキの設計で大きく取り上げられることが無かった、ディスクの回転速度を考慮したブレーキシステムの不安定鳴きモードのシミュレーションプロセスの説明と、その計算結果について報告を行う。
本稿で用いられる計算手法による計算によれば、ディスクの回転速度に応じて相当減衰率が大きく変化すること、すなわち、回転速度に応じて複素固有モードの状況も変化し得ることが判明した。このことから、たとえ、ある回転速度でブが安定性を示していても、停止寸前の低い回転速度になると、不安定鳴きモードに転ずる可能性があることを示唆している
ここでは、車両への装着を想定したブレーキについて一般に広く用いられる3次元有限要素解析モデルを用い、シリンダーとピストン間に、低速走行時負荷として想定される比較的高い液圧を与えた。本計算手法では、ディスクとパッド間にはバネを挿入せず、接触解析によって得られた計算結果から、接触箇所に対してMPC(多拘束)によって自動的に結合するコンタクトロッキングなる手法により、アセンブリパーツの結合を行い、ブレーキシステム全体に対する不安定鳴きモードの有無について調査した。
2.ブレーキ鳴き解析のプロセス
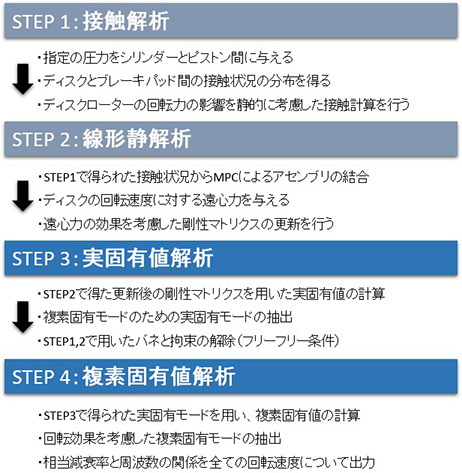
図-1 ブレーキ鳴きの解析フロー
ブレーキ制動時に発生する異音、いわゆるブレーキ鳴きがどのような条件で現れるかをシュミレーションで予測するために、本稿では、図-1に示すフローに従い計算を進めた。
STEP1は、接触解析であり、非線形境界問題を静的な荷重状態を想定し計算を行う。ここで得られる接触状況は本ステップの計算結果として最も重要な情報と考えられるが、要素サイズを詳細にして、解像度の高い接触状況を得ようとした場合、計算時間が増大するという現実的な問題に直面する。
STEP2は、接触解析である。本来、複数のアセンブリパーツに対し、固有値解析などの振動計算を行う場合は、何らかの手法により全パーツを一体化する必要がある。ここでは、コンタクトロッキングと呼ばれる手法により、接触境界面に存在する節点のうち、接触した節点のみを接触した相方の要素とMPC結合(多点拘束)し一体化を図る。このアセンブリに対し、遠心力が生じる為に得られる応力寄与効果を、剛性マトリックスを更新することで表現する。
STEP3は、実固有値解析であり、実固有モードの抽出が主な目的である。ただし、静的計算の安定化のために用いた設定は全て解除し、更新後の剛性マトリクスにより固有値計算を行う。
STEP4は、複素固有値解析であり、STEP3で求めた実固有モードをベースに複素固有モードの抽出を行う。ただし、回転速度の影響を確認するため、ディスクローターの回転速度のレンジを事前に設定し、各回転速度に対するモード特性を把握するため、キャンベル線図の生成を行う。
ブレーキの複素固有値解析を行えば,計算結果として相当減衰比率が得られる.ブレーキの不安定鳴きモードの指標である相当減衰比率:DRは、式-1より求められる値であり,正値のとき安定モード,負値のとき不安定モードと判定される.
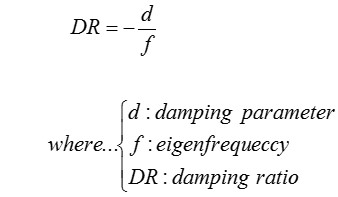
式-1
3.ブレーキ鳴き解析のためのマトリクス方程式
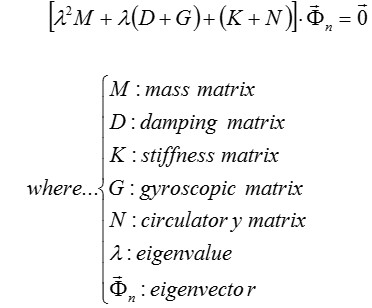
式-2
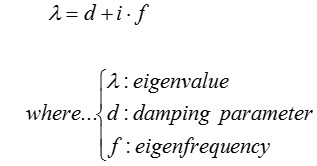
式-3
ブレーキ鳴きの現象は、ブレーキシステムの動的不安定性により誘発されるものであり、システム全体が自励振動のエネルギーを抑制できなくなり、その果として音波が放出されると考えられている。
ブレーキのシステム全体にかかわる動的特性を厳密に評価するために,式-2に示す回転効果を考慮したマトリクス運動方程式を用い、複素固有値解析を実施した。
回転効果が含まれるマトリクスとして、式-2における、ジャイロマトリクス:G,循環マトリクス:N,およびディスクローターの回転速度に伴う遠心力を考慮するための幾何剛性マトリクス:K の3つが挙げられる。
なお、式-3に示される式よって、減衰マトリクスが固有値に対し影響を及ぼすことが分かる。
本稿では、あくまでも、ディスクローターの回転速度と動的安定性をテーマとして検討を進めるが,通常,ブレーキ鳴き解析では、ブレーキ液圧の値を設定し、測定値と比較をしながら、ディスク-パッド間の摩擦係数などをパラメトリックに求めることが多い。
また、ブレーキパッドに代表される摩擦材の動的特性については、異方性を示すことが一般に知られており,式-4に示される面内等方性材料モデルがよく用いられる。ここでは、動的応答試験の測定値と数値シミュレーションの合わせ込みにより、全てのポアソン比をゼロとし、対角項のみに値が入る、式-5の材料構成則を用いて検討を進めることとした。

式4-5
4.ブレーキ鳴き有限要素解析モデル
(1)ブレーキ鳴き解析モデルの概要
ブレーキ鳴き解析を精度良く効率的に行うため、ここでは、図-2に示す有限要素モデルを用いた数値シミュレーションを行った。モデル規模および計算に用いたマシンの仕様を以下に示す。
- ◆モデル規模
部品点数:13, 節点数:781,076,要素数:576,221 接触ペア数:58,257 - ◆マシン仕様
コア数:24,メモリ容量:256GB,ディスク容量:4TB(SSD)
有限要素モデルのメッシュには、主に10節点テトラ2次要素を用い、ピストン・パッド・ディスクなど接触近傍部には、8節点ヘキサ1次要素を用いた。
図-1で説明した解析フローの全プロセス(接触解析から複素固有値解析までを、1~60km/h の回転速度に対し、1km/h 刻みで60個の計算結果を出力)に要した計算時間は、トータルで約50分程度であった。
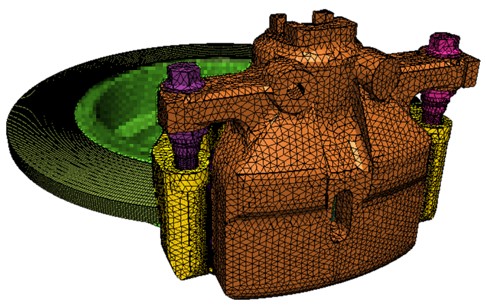
図-2 有限要素モデル
(2) ブレーキ鳴き解析の詳細
STEP1の接触解析では、ディスク-パッド間のみならず、パッド-ブラケット間など、接触が生じる可能性のある箇所に対する接触定義を心掛けた。著者らの行った既往の研究では、アセンブリパーツに対する接触-振動連携解析において、静的解析により得られる接触状況を的確に捉え、接触圧力に依存した結合剛性を用いることで、後続の振動特性について高い精度でシミュレートできることを確認している。ただし、ここでは、ブレーキの振動現象と回転項の影響を中心に調べるため、接触部は全てMPCによって剛結する一般的な手法を用いている。
STEP2の線形静解析では、STEP1の接触解析で検知された接触境界の節点に対するMPCが自動生成され、パーツ間の結合が完了した状態に対して、ディスクの回転に起因する遠心力の影響を初期応力効果として加えた剛性マトリクスの更新が行われる。
STEP3の実固有値解析では、STEP2の線形静解析で使用したモデルから、接触計算を行う際に剛体移動の阻止を目的として設定したバネ要素を全て除去し、STEP2で得られた更新後の剛性マトリクスを用いて、0~15,000 Hzの周波数帯域を対象とした実固有解析を行った。
STEP4の複素固有値解析では、STEP3の実固有値解析で抽出した固有モードを用い、動的回転問題に対する計算を行う。ここでは,ディスクローターの回転速度をある範囲で指定し不安定鳴きモードの特性を調べる。具体的な安定性の判定は、式-1で示した相当減衰率の分布を用い、相当減衰率が判定基準値を下回れば、ブレーキに不安定鳴きモードが現れると仮定した。また、回転効果の影響を詳細に確認するために、相当減衰率と回転速度の関係を表すキャンベル線図を出力した。その他、相当減衰率の分布結果から、計算条件の範囲内で、最も不安定なモードにおける、動的挙動を確認するため、ひずみおよび運動エネルギーの密度分布を出力した。
5.ブレーキ鳴き有限要素解析モデル
(1)接触解析(STEP1)の計算結果
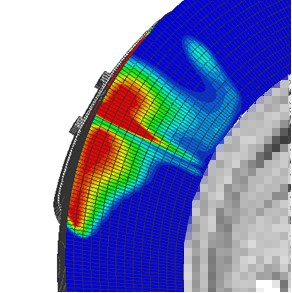
図-3 ディスクに生じる接触圧分布状況(青は最小値:0MPa、赤は最大値:1MPa)
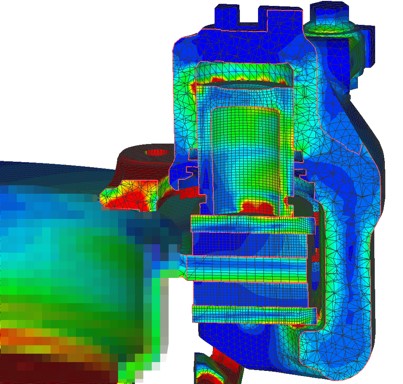
図-4 ミゼス相当応力分布状況(断面図)(青は最小値:0MPa、赤は最大値:10MPa)
STEP1では、3 MPaのブレーキ液圧をシリンダーとピストンに与え、パッドとディスク間に生じるすべりによる接触を厳密に評価し、後続の振動解析のための接触状況を得ることが最大の目的である。図-3に示すように、パッドとディスクの接触により接触圧分布が生じ、液圧によるディスクの圧縮状態が確認できる。また、ブレーキシステム全体に分布する応力状態についても、図-4(断面図)の結果から把握できる。
(2)静的解析(STEP2)の計算結果
STEP1で得られた接触状況から、ブレーキのアセンブリパーツはMPCによって結合され、その結合状態に対し、ディスクローターの回転に伴う遠心力を与える。計算後に出力されるログファイルの記述内容より、後続の実固有値解析に必要な要素剛性状態をアップデートされたことを確認した。
(3)実固有値解析(STEP3)の計算結果
STEP3では、STEP2で既に生成されたMPCによって、マルチボディの結合が自動的に行われた状態である。ここでは、STEP2でアセンブリモデルに与えた遠心力の影響を考慮した応力状態を反映するため、更新後の剛性マトリクスにより実固有値解析を行う。STEP2の静的な力の釣合条件を満たす目的で用いられた拘束条件やバネ要素は全て除去し、周波数帯域を0~15,000Hzとしたフリーフリーの実固有値解析を実施した。その結果、1番目の固有モードは116Hz、最後の208番目の固有モードは14,896Hzに現れた。
(4)複素固有値(STEP4)の計算結果
STEP4では、STEP3で得た実固有モードの計算結果を基に、周波数帯域を0~15,000Hzとした複素固有値解析より、208個の共役な複素固有モードを得た。なお、本稿のテーマである回転効果の影響とブレーキの鳴きモードとの関連性を調べるために、ディスクの回転速度(1~60km/h)と抽出される鳴きモードについて詳細に評価するため、次の3項目について確認した。
- (a)相当減衰の分布
ディスクの回転速度が低いときの相当減衰率の分布状況を確認するため、図-5の回転速度が1km/hのときの相当減衰率の分布を確認した。ここでは、減衰率が負値となる不安定モードが、この回転速度の場合、10個発生していることが分かる。 - (b)相当減衰率と回転速度の関係(キャンベル線図)
図-6(もしくは図-5)の相当減衰率の分布により、ディスクの回転速度を1km/hとしたときの、ブレーキの不安定鳴きモードを視覚的に特定できるようになった。図-6に示された①~③の不安定鳴きモードは、図-7①~③に示したキャンベル線図にそれぞれ対応する。
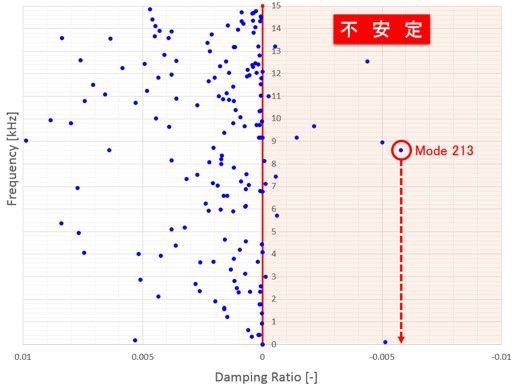
図-5 相当減衰率分布(横軸:周波数)(ディスクの回転速度:1km/h)
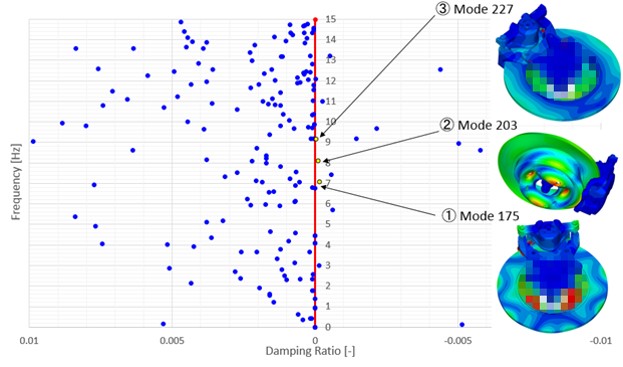
図-6 相当減衰率分布とブレーキの鳴きモード図(ディスクの回転速度:1km/h)
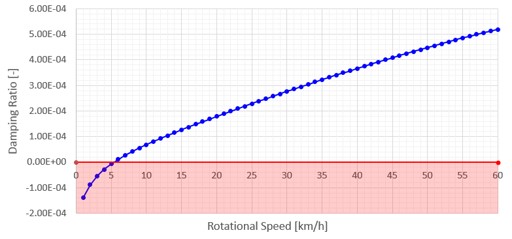
図-7 ① 相当減衰率キャンベル線図 (1~60km/h)
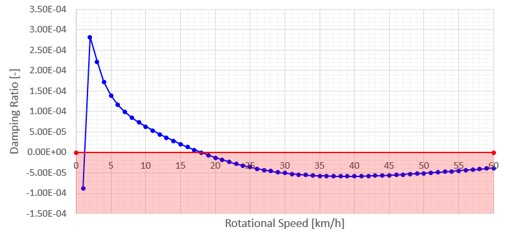
図-7 ② 相当減衰率キャンベル線図 (1~60km/h)
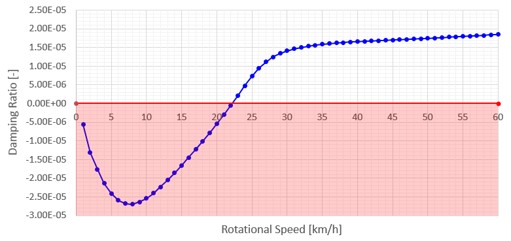
図-7 ③ 相当減衰率キャンベル線図 (1~60km/h)
図-7 ①~③に示された相当減衰率に対するキャンベル線図によれば、本稿の冒頭で述べた、車両が極めて低速に走行した場合に、相当減衰率が負荷を示しブレーキが不安定鳴きモードになり、速度が増すにつれ次第に安定側に移るという傾向が確認できる。換言すれば、仮にある程度速度が出ている状態で安定モードであっても、ブレーキ制動に伴う減速により、ローターの回転速度が低くなれば不安定鳴きモードに転じてしまう可能性を示唆している。
上記のような、低速時に不安定鳴きモード、高速時に安定モードを示すケースは、図-6の①~③の分布位置からも分かるように、相当減衰率がゼロより僅かに大きく、7,000 Hz 以上の周波数という条件下で起こる傾向にあることが分かる。なお、図-7 ①のように、相当減衰率が回転速度の単調な増加関数として表される場合もあれば、図-7 ②、③のように、回転速度の低いゾーンで、変化率が複雑に変化しピークが現れる可能性もあることが分かる。
ここで得られた計算結果より、回転速度が低いという理由で、回転効果を無視したブレーキの安定性の評価を行うことは、安定性に対する厳密な評価ができないということが分かる。
(c)不安定泣きモードのエネルギー密度分布
ここでは、図-5に示した相当減衰率分布を用い、最も強く不安定鳴きモードが現れた、Mode 213(周波数8,609 Hz)を対象にして、運動エネルギー密度分布、ならびにひずみエネルギー密度分布について確認を行い、それらに関する各ブレーキパーツの寄与率について調べた。
図-8と図-9に示されるブレーキのひずみエネルギー密度分布、および運動エネルギー密度分布図により、視覚的かつ直感的に分布状況を確認した。また、ここでは、各分布に対する寄与率を算出し、円グラフにして結果を示している。図-8から、リテイナー(薄い金属プレート)のひずみエネルギー密度が最大寄与率を示すことから、この不安定鳴きモードにおいて、曲げ変形が大きくなることが予想される。また、図-9の運動エネルギー密度分布の結果から、ブレーキ鳴き現象の象徴的兆候であるディスクとピストンに大きな運動エネルギーが生じていることが確認できる。
6.結論
本稿では、ブレーキの不安定鳴きモードの計算の際に、ディスクの回転効果が、ブレーキの安定性に大きな影響を与えることを、相当減衰率の分布、および相当減衰率のキャンベル線図を用いて明らかにした。本検討により得られた主な知見をまとめると以下のようになる。
- 1) ブレーキ鳴き解析を行う場合、回転効果を無視した計算を行うと、回転速度に応じて変化する相当減衰率の値を正当に評価できなくなる
- 2) ディスクの回転速度がゼロに近い場合であっても、モードの安定性が急転する可能性があるため、キャンベル線図などを用いた確認が有効である
- 3) ディスクの回転速度(1~60km/h)を全て考慮した、接触解析から複素固有値解析までに至る、ブレーキ鳴き解析を行い、50分という現実的な時間で、計算結果を得られることが分かった
今後は、本稿で行ったディスクローターの回転速度とブレーキの不安定鳴きモードとの関係について、タイプや形状の異なるブレーキモデル、使用上想定されるブレーキ液圧、ならびに現実の走行状態に応じた回転速度による検討などを行い、実際のブレーキ鳴き挙動から得られる傾向や測定値との比較から、本ブレーキ鳴きシミュレーション手法の妥当性の検証を進める方針である。
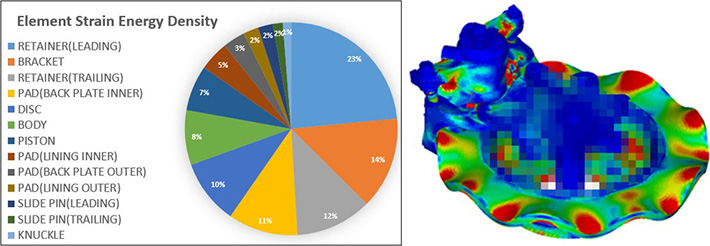
図-8 ブレーキのひずみエネルギー密度分布状況およびその寄与率
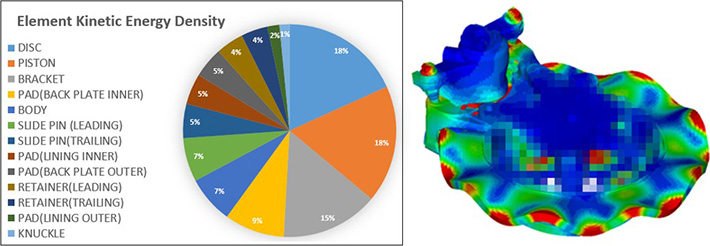
図-9 ブレーキの運動エネルギー密度分布状況およびその寄与率
