界面要素を使用した接触-振動連携解析
下薗 征史 博士(工学) インテスジャパン株式会社 代表取締役
芦田 克彦 日信工業株式会社 主幹
増田 千尋 日信工業株式会社
斉藤 絵美 インテスジャパン株式会社 チーフサポートエンジニア
1 接触圧の影響を考慮した振動解析
1.1 接触-振動解析を行う理由
自動車や飛行機など輸送機器の大部分は、複数部品からなるアセンブリモデルであり、位置調整、応力緩和、品質劣化の際の部品交換などの目的で、境界面を完全に結合せず、敢えて接触による一体化を用いる場合がある。接触によるアセンブリの一体化は、接触境界面に発生する接触圧分布の解明が重要なテーマとなるが、アセンブリモデルにおける接触面数が増加すれば、非線形性も高くなることから、静的にも動的にも接触面を数多く含む力学的挙動の予測は困難である。今日、有限要素法をベースにした数値シミュレーションによる検証は、ものづくりの現場ではスタンダードな手法であり、とりわけ部品点数が多く、異なる材料特性を有する変形体から構成される大規模なアセンブリモデルは、汎用構造ソルバーの使用用途として最も相応しいと考えられる。
本研究の主な目的は、大規模アセンブリモデルに対する周波数応答解析を、ものづくりの現場での使用を想定し、計算時間が現実的であり、計算精度が実現象を高い精度でトレースできる、接触-振動連携解析手法の確立を目的としている。
従来の大規模アセンブリモデルの伝達関数の計算では、部品間の境界面は、そのままMPC(多点拘束)で結合された計算モデルを加振することにより、応答特性を評価していた。そのため結合部は現実よりも高い剛性を示すこととなり、動的挙動の正しい評価も困難であった。
近年、いくつかの汎用構造ソルバーでは、上記の結合剛性の問題を克服するために、静的解析の結果として得られる接触状況を利用し、接触/非接触でMPC結合のオン/オフをスイッチングする機能が新たに実装された。本機能を使用する場合、境界面における接触状況を厳密に表現するために、なるべく詳細な要素分割が求められるが、振動試験で得られる応答特性を、比較的高い精度でシミュレートできる有効な手法として期待できる。
上記手法を用いることで、応答伝達関数の精度面に対する問題は大きく改善されるものの、大規模アセンブリモデルの課題として、接触面の節点数の増加に伴い、接触計算の負荷が高くなるという問題に直面する。つまり、精度を求めれば計算コストが犠牲になるという一種のトレードオフ問題に陥る。また、摩擦を伴う接触問題になれば、接触自由度の増大はより深刻な問題になる。
本稿で提案する接触-振動連携解析の手法は、計算の精度と速度のトレードオフ問題の解決について、有効な手法と考えられる。接触境界面を複数含むアセンブリモデルにおいて、接触面で得られた接触状況および接触圧に着目し、計算収束性の向上のため、接触境界面の要素には、ある程度ラフなサイズのものを用いた。ここでは、実際のブレーキのアセンブリモデルを対象として、動的応答試験の結果と解析結果の比較を行い、本稿で提案する解析手法の妥当性を検証した。
1.2 接触-振動解析の計算プロセス
図-1に、ブレーキのアセンブリモデルを用いた接触-振動連携解析の計算プロセスを示す。4つの計算ステップは、1つのジョブ内で、接触解析、線形静解析、固有値解析、周波数応答解析の順に連続的に実行することが可能である。
ただし、振動試験で得られた応答関数に対するカーブフィッティングを行う場合、1.3で説明する界面要素の材料パラメータのためのスタディがある程度必要になることから、スタートのステップ1に戻らず、途中のSTEPからリスタート(再計算)を行っている。
このリスタート機能を積極的に用いることで、動的な材料特性の変更を行った計算時間は大幅に短縮され、材料特性の同定プロセスの高速化が図れる。動的剛性の変更の場合はリスタート①、減衰定数の変更の場合はリスタート②からの計算の実行が可能である。
1.3 ペンタ2次要素による界面要素モデリング
著者らの既往の研究でも、接触-振動解析に対する界面要素の適用の可能性について、8節点ヘキサ1次要素を用いた検討を行ったが、ここでは、18節点ペンタ2次要素を用いた新しい界面要素の適用の可能性について検討を行った。ペンタ2次要素を使用する利点は、まとめると概ね以下のような内容になる。
- 1) 設計現場では、ほとんどの場合、3次元CAD形状に対しテトラ2次要素によるメッシングが用いられる為、界面要素を作成する場合、要素面が四角形で構成されるヘキサ要素よりも、三角形で構成されるペンタ要素を用いたメッシュ作成が容易になる
- 2) 10節点テトラ2次要素とペンタ2次要素も、ともに中間節点のある要素の為、異なる要素タイプであっても連続性が高く整合性を損なわないモデリングが可能である
- 3) 18節点ペンタ2次要素は、要素層方向に中間節点を有す要素である為、単一レイヤーであってもせん断ずれに対する変形挙動を柔軟に表現できる
さらにここでは、中間節点の存在が接触計算の収束性を低下させる問題を克服するため、中間節点と主節点の相対位置関係をMPCで関連付ける機能により、接触計算の収束性の向上を図った。
ブレーキのアセンブリモデルに用いる界面要素の拡大図を図-2に示す。
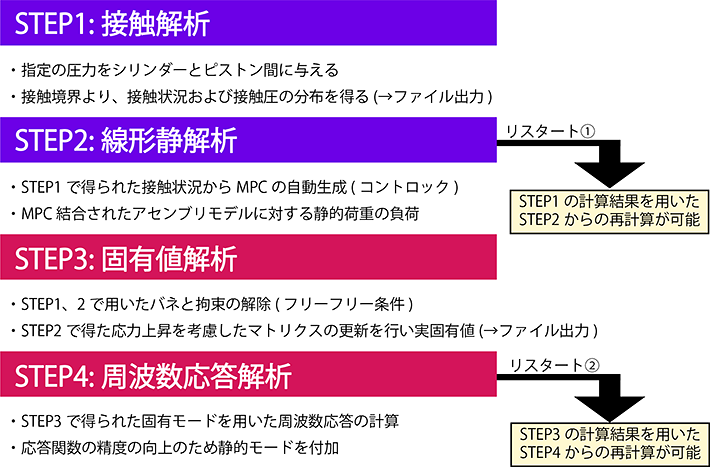
図-1 接触-振動連携解析のプロセス
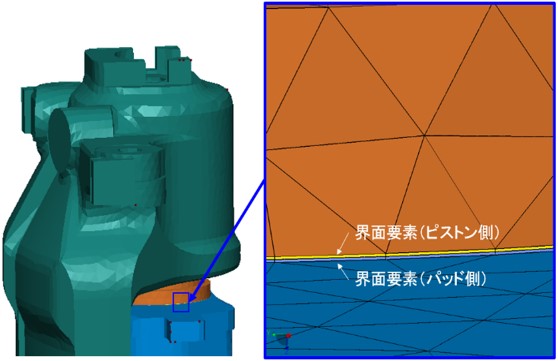
図-2 界面要素のモデル状況
1.4 界面要素の動的材料特性の考え方
1.3で述べた界面要素に与える材料特性は、接触解析と動的解析でその扱いを変えた。
接触解析では、一般的な等方性弾性材料、一方、動的解析では、直交異方性弾性材料を用い、接触解析で得られた要素の平均接触圧に依存した動的な材料特性を用いた。
図-3にモデル内における界面要素の全体的な配置状況を示す
界面要素に用いる動的特性は、要素の縦/横剛性、および減衰率がいずれも平均圧力の関数で表現されると仮定し、接触面の構成節点が全て非接触であれば、界面要素間にMPCは生成されず、剛性および減衰係数は、母材の静的特性に完全に一致すると仮定した。
図-4に界面要素に生じる平均圧力と材料特性の関係を示す。

図-3 界面要素の配置状況
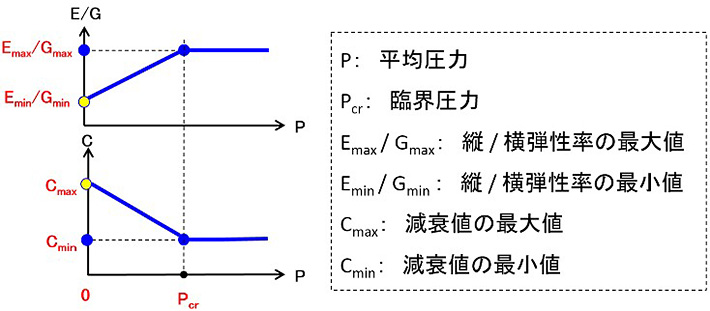
図-4 界面要素に生じる平均圧力と材料特性の関係
応答試験は、ピストン液圧が1.0(MPa)負荷された状態で行われており、界面要素の動的材料特性を示すパラメータのチューニングは、試験と解析の相関性をFRAC(周波数応答信頼性基準)値を比較することにより行っており、界面要素の動的な材料構成則は、式-1のように与え振動計算を行った。
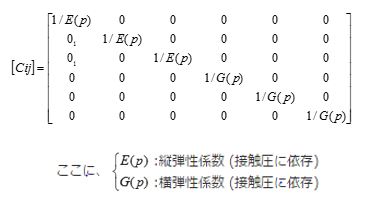
式-1
2 接触-振動連携解析の計算事例
2.1 ブレーキパーツモデル
1.2で説明した計算プロセスに従い、図-5の有限要素モデルを用いた接触-振動連携解析を行った。計算に用いたマシンのスペックを以下に示す。全プロセスに必要な計算時間は約30分程度であった。
- ◆モデル規模
部品点数: 5 (界面要素を除く)
節点数: 661,510 要素数: 439,231 接触自由度: 7377 - ◆マシン仕様
コア数:24 メモリ容量:256GB ディスク容量:4TB(SSD)
メッシュサイズの平均:約3mm
(接触近傍部は約2mm)

図-5 有限要素モデル
2.2 静的解析結果
図-1(接触-振動連携解析の計算プロセス)で述べたSTEP1では、ブレーキ液圧に相当する圧力荷重1.0MPaを所定の密閉領域に与え、ディスク底面の節点自由度を完全拘束、ピストン、パッド、ディスク、キャリパに至る一連のパーツ間には摩擦を考慮した接触条件を与え計算を行った。
なお、本稿に用いたパッドは、通常ブレーキパッドに用いられる異方性材料ではなく、等方性材料を用いており、振動試験に用いたパッドの材料(標準的な鋼材を使用)に合わせている。図-6に計算結果の一例としてミゼス相当応力の分布状況を示す。
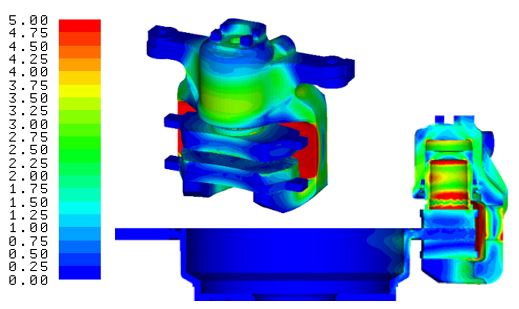
図-6 ミゼス相当応力分布状況 (単位: MPa)
2.3 動的解析結果
STEP4の周波数応答解析結果の計算精度については、式-2に示すFRAC(Frequency Response Assurance Criteria)値により検討を進めた。FRACアセンブリモデルの11箇所について、加振点および加速度を計測する応答点を設定し、応答特性の比較は、応答点におけるイナータンスを用いて行った。表-1に各計測点におけるFRAC値の傾向を示す。

式-2
ここでは、アセンブリパーツ間の動的特性と接触圧分布の関係を調べるため、界面要素の材料は接触圧に関係なく常に母材と同じ特性を有すCLK(コンタクトロッキング)モデルのFRAC値についても調べた。図-7に一例として、11箇所の計測点中、界面要素モデルとCLKモデル間でFRAC値の差が最大(44.6%)となる周波数応答関数の比較のグラフを示す。
界面要素を含むブレーキのアセンブリモデルより、図-1で示した同定プロセスを経て、全計測点のFRAC値の平均が50%を越える良好な結果を得た。最終的に得られた界面要素の動的材料特性表-2に示す。
3 計算結果の考察と結論
3.1 計算結果の考察
まず、2.2の静的解析の計算結果により、圧力荷重を1.0MPaに設定した接触解析の結果は、図-6の相当応力の分布状況より、ピストンからキャリパに至る一連のパーツに伝達し、接触力が正しく伝わっていることが、モデルの断面図などから視覚的に確認できる。
次に、2.3で得られた動的解析の計算結果から、 接触面をMPCで結合したCLKモデルにより応答特性を求める場合、接触状況を詳細に表現できる有限要素モデルを用いなければ、接触面の結合剛性を過大に評価し、現実の傾向とは異なる応答特性が現れることが分かる。一方、接触圧に依存した動的な材料特性を界面要素に導入した計算を行えば、FRAC値が大きく向上することが確認できた。
3.2 結論
本稿で提案した、アセンブリモデルに対する界面要素を用い、接触圧を考慮した振動解析を行った。得られた知見をまとめると以下のようになる。
- 1) 接触解析から周波数応答解析に至る、複数の解析タイプの計算を30分程度で行えることが分かった
- 2) 接触圧に応じた材料特性を、界面要素の動的な材料特性として用いることで、アセンブリモデルの応答特性の精度が向上できることが分かった
- 3) 界面要素の動的特性を得るためには、材料パラメータの同定がある程度必要であるが、接触-振動解析における一連のプロセスを、途中の段階からスキップすることで、時間短縮が図れることが分かった
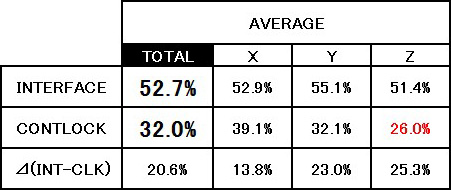

表-1 各側定点におけるFRAC値の傾向
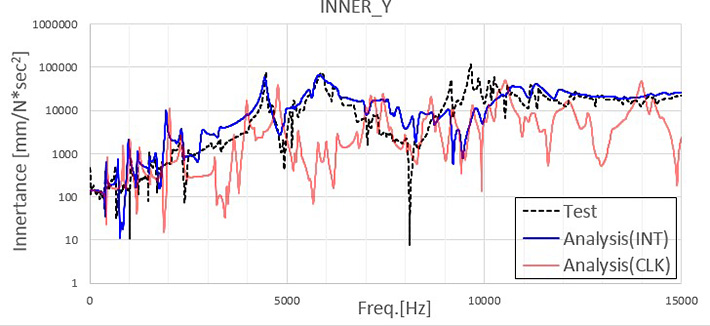
図-7 周波数応答関数の比較(0~15,000Hz:INNER-Y)
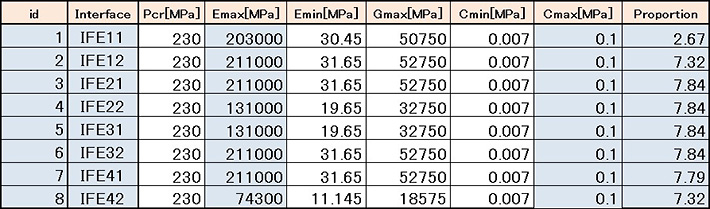
表-2 界面要素の動的材料特性
