有限要素解析ソルバー:PERMASモジュール
PERMAS-MQAは基本モジュールであり、その他すべてのPERMASモジュールのためのシステムカーネルとなります。 このシステムカーネルは、特に、次のものを提供します。
- データ管理システム、UCIコマンド言語、
- PERMASモデルの標準入力、結果の標準出力、
- モデルの整理統合、サブストラクチャリング、
- 多数の要素タイプ、高速ベクトルルーチンツールなど
PERMAS-MQAの特徴は、解析プロセスの品質保証を確かにするというコンセプトとツールにあります。
- ・ 今日の製品開発において、有限要素解析は複数の設計バリアントを早期に評価し、開発プロセスを加速するために用いられています。
- ・ FEAシステムに対するスキルはエキスパートに対するスキルというより、より一般的な基礎技術となっています。
- ・ FEアプリケーションは、ますます複雑なものになってきています。
ソフトウェア品質に加えて、FEAの結果に対する信頼性は次の点に依存します。:
- ・ 包括的なモデル検証: PERMASは、入力データの非常に徹底した検査を行います。数千もの異なるプレーンテキスト形式のシステムメッセージを提供し、 複雑な矛盾点に対応して適切に出力されます。特に、特異性の自動検出機能は、ユーザーの作業時間の節約に大いに役立ちます。
- ・ エラーを含む解析実行の回避: PERMASには、エラー実行を回避するためのタスクスキャン機能が実装されています。:
- 解析ステップごとにチェックが行われ、解析全体としての実行可能性が検証されます。
- 解析実行に先立って、CPUタイムとディスク容量というコンピュータリソースの見積りが行われます。
- 要求された解析ステップにおける入力モデルデータにおける完全性と整合性がチェックされます。
- 使用するプラットフォームにおいて、ライセンスが発行されていないPERMASモジュールに対してさえチェックすることができます。
- ご使用のプリプロセッサにおいてモデルチェックを行うことで、本機能により、よりいっそう厳密なモデルの検査が行えます。
- ・ ユーザーの作業負荷の軽減: 快適な入力方式、ダイレクトインターフェイスおよび上記のモデル検証ツールによって、面倒なルーチンワークが軽減され、 モデルに関連するすべての情報の概要を容易に知ることがでます。その結果、ユーザーは解析目的と結果評価に集中することができるようになり ます。特に、プリプロセッサからのモデルデータのスムースな転送が、快適なインターフェイスによってもたらされます。
SDM(Simulation Data Management)は、システムによる通信を、コメント機能によって補助します。 このコメントは、モデル定義中の任意のエンティティの記述に対して、自由に意味を持たせる機能を提供します。 そのため、モデル入力に含めるか、または外部ファイルとして付加することが可能です。外部ファイルとしては、 XML形式を使用することもできます。
Porsche社(Weissach)の提供
このモジュールでは、微小変位、微小ひずみ、および線形材料挙動(等方性または異方性) の仮定に基づく線形弾性解析が可能です。したがって、このモジュールは有限要素解析の最初のステップとしてよく用いられます。
- ・ 次のタイプの運動学的境界条件が利用可能です。: - 自由度の抑制
- 強制変位
- 線形拘束(MPC)
- ・ 不拘束または部分的な不拘束を有する構造に対しては、準静的解析(慣性リリーフ)を実行できます。 この解析では、剛体運動を分離することにより、載荷荷重と釣り合うような慣性力が計算されます。 続いて、載荷荷重とこの慣性力のもとで静解析が実行されます。
- ・ 様々な種類の静的荷重が利用可能です。
- ・ 次の一次結果が計算されます。: - 変位
- 質量および慣性モーメント
- ・ 要求により、次の結果の計算が可能です。: - 反力
- 応力および合応力
- ひずみ
- 残差力
- ひずみエネルギー密度(質量または体積当たりのひずみエネルギー)
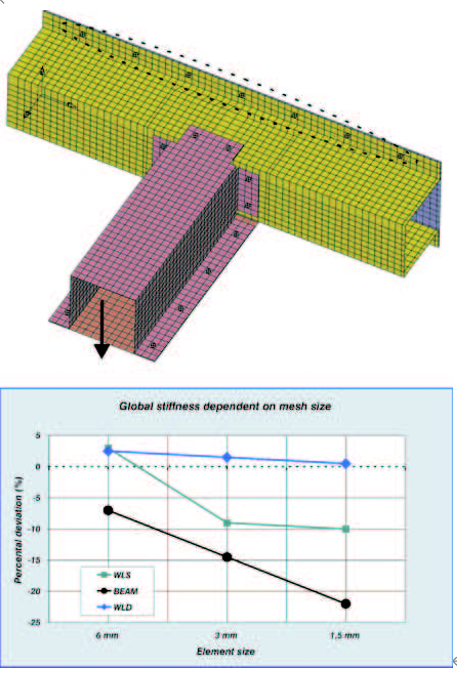
このモデリング法により、全体的な剛性を適切に表現することができます。
しかしながら、溶接線に沿ってスポット溶接部の反力が様々にかつ大きく変化する可能性があります
例えば、フランジ間が不整合メッシュであることによる影響)。
このモジュールは、モデル定義のスポット溶接部の反力への影響および剛性の表現を改善した、
改良スポット溶接モデルを提供します。このモデルは、剛性を内部的に調整するために3次元モデルを用いています。
PERMAS-CAモジュールにより、非線形境界条件(接触問題)を含む静解析を実行できます。
接触境界条件は、弾性体間または弾性体と剛体の間に定義できます。
また、ボディには非線形挙動を含めることができます。
接触を定義するにはいくつかの方法があります。:
- ・ 接触節点ペアの指定
- ・ 各接触ゾーンに対する節点セットの指定(節点ペアは自動的に検出されます)
- ・ 節点/節点セットのサーフェスへの割り当て(不整合メッシュ)
- ・ 一般的な面-面接触定義(不整合メッシュ)
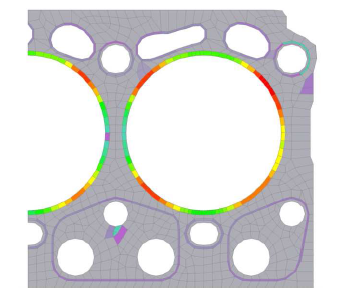
不整合メッシュに接触を定義する機能によって、接触するボディ間のメッシュサイズを自由に与えられるようになります。
これによって、下図(不整合メッシュの接触)のような接触圧を厳密に評価する必要のある場合に対し、特別なモデリングも可能になります(ギア歯の接触などに有効)。
接触方向および初期ギャップ量は、明示的に指定することも、幾何形状から自動的に決定させることもできます。
圧入については、負のギャップ量を指定することにより容易に表現可能です。
接触解析では、クーロンの摩擦法則に従い、固着または滑りを伴う等方性または異方性の摩擦接触の考慮も可能です。
荷重履歴を指定することによって、アセンブリ、作用荷重および任意の接触状態のシミュレーションを、
滑りおよび固着現象を考慮した摩擦モデルとして正確に行うことができます。
これにより、そのような状況を準静解析の範囲で容易にシミュレーションできるようになります。
荷重履歴は、ポストスクリプトプロットファイルに書き出し、グラフィカルに表示できます(荷重履歴の表現をご参照)。
荷重履歴に(例えばボルト締めなどの)プリテンションを考慮することができます。
その場合、プリテンションを考慮する際に接触解析が行われます。
同様に、スクリュー締めトルクが、スレッド領域の既知の接触力によってモデル化されます。

ボルトプリテンションには一般的な概念が導入されています。
法線方向のプリテンションのために切断面を用いる従来のアプローチに加えて、
軸方向のプリテンションを円筒状のスレッドに関連させた新しいアプローチが利用可能です。
この非常に画期的な機能によって、スレッド部のフランク角およびピッチの形状に起因した半径方向の広がりと軸トルクの詳細な効果を、
詳細なメッシングを用いずとも容易に定義できるようになります(ボルトプリテンションをご参照)。
接触タイプ、その幾何形状(ギャップ量および法線ベクトル)、
そして接触座標系(法線方向と摩擦方向を規定)のような接触モデルを検証するための包括的なチェック機能が実装されています。
さらに、すべての反復ステップで接触状況を出力させ、チェックすることができます。
摩擦接触では、接触面のクオリティが非常に重要なファクターとなります。
そのため、PERMASには摩擦挙動の抜本的な改善のために接触面を平滑化するスムージング機能が実装されています。
解析の過程で、接触自由度から導出された縮約モデルが用いられます。この処理の利点は次のとおりです。
- ・ 反復計算が非常に効率化され、相当数の接触節点を有する大規模モデルに非常に有益です。
- ・ 余分な剛性が接触のモデリングによって誘起されることがなく、解析結果の精度は十分保証されます。
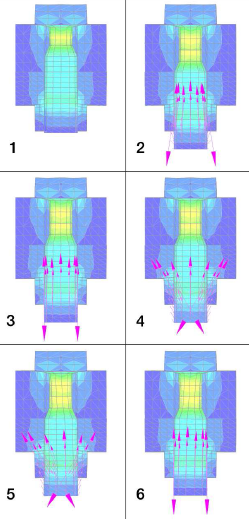
変形した中型ねじの節点応力とプリテンション力:
-
1 ボルトの切断面表示
2 半径方向に結合させたスレッド
3 半径方向に結合させないスレッド
4 フランク角付き(ただし、ピッチ角なし)のスレッド
5 フランク角とピッチ付きのスレッド(M10規格)
6 ピッチ付き(ただし、フランク角なし)の左巻きスレッド
複数の荷重ケースを同時に解析することが可能であり、荷重ケースの数は任意です。 荷重ケースごとに接触パラメータ(例えば、ギャップ量や摩擦係数)を変えることもできます。 接触境界条件は、静解析の過程で自動的に考慮されます。ユーザーは特に接触解析を指示して実行することはありません。
接触状況ファイルを生成することにより、一連の接触バリアントを効率良く計算することができます。
接触状況ファイルは、ジョブのリカバリを容易にし、かつ計算実行時間を大幅な短縮を可能にします。
静解析から得られるすべての結果に加えて、接触解析では、接触状態、接触力、接触圧(接触する2つの物体の温度分布を参照)、
ギャップ量、相対ギャップ変位などを出力します。
後続の解析のために、接触状況をロックすることできます。この接触ロッキング機能により、現状の接触状況に基づいたMPC(線形拘束)が自動生成されます。 新しく生成されたモデルによって、後続の解析(例えば、固有値解析、熱伝導解析、またはサブモデリング解析を中断なく連続的に実施することが可能です。
このモジュールは、大掛かりな固着-すべり問題や大規模接触モデル(10万接触ペア以上)に対して、 接触解析の実行を劇的に加速させるための新しい接触計算アルゴリズムを提供するために開発されました。 このモジュールは、PERMAS-CAモジュール(前節をご参照)のアドオンモジュールとして用いられます。
次のような機能が提供されます。:
- ・ ハイパフォーマンスな反復計算アルゴリズム: 標準の摩擦接触解析を高速化します
- ・ 非常に安定した特別な反復法: 厳密な固着-すべり問題に対応します(例えば、すべての接触ペアが滑り状態になる場合、下図(円錐の圧入問題(挿入後のすべり摩擦力))を参照。
ガスケット要素を、非線形材料解析のルーチンではなく、接触解析の反復計算のルーチン内で処理できるようになりました。
この機能により、実行時間が従来の解法に比べて著しく低減できます。特に、モデル中の非線形性が接触およびガスケット要素のみ
である場合、実行時間の低減はより顕著です。たとえ、接触およびガスケット要素以外に非線形性が含まれていたとしても、
実行時間は大きく節減されます。
動的に可動する部品間の滑り摩擦問題に対し速度場を規定して、 すべり問題を準静的な接触解析の範囲で解析することが可能です。
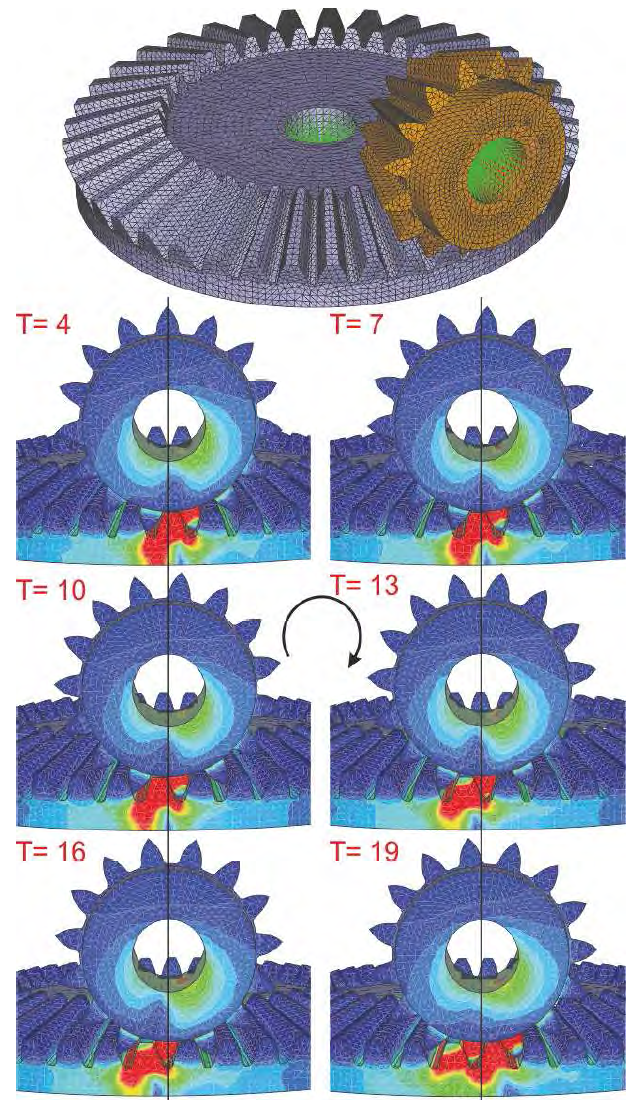
このモジュールでは、有限すべり接触問題に特別に対応するため、新たな接触解法アルゴリズムが提供されています。 以下に挙げるような状況では、有限すべり接触解析機能による更新作業が必要になります。
- ・ 接触する変形体同士の大きな相対変位を考える場合、接触状況を更新すること、 変形体間の相対変位を適切に反映します(接触情報更新のためのクリップの例題と主動ギアと従動ギアを参照)。
- ・ 仮に非常に高精度な接触の結果が求められる場合には、接触状況の更新を行うことで、 接触力、変位、応力などの接触情報に関する、きわめて微小な変化であっても確実に反映します。
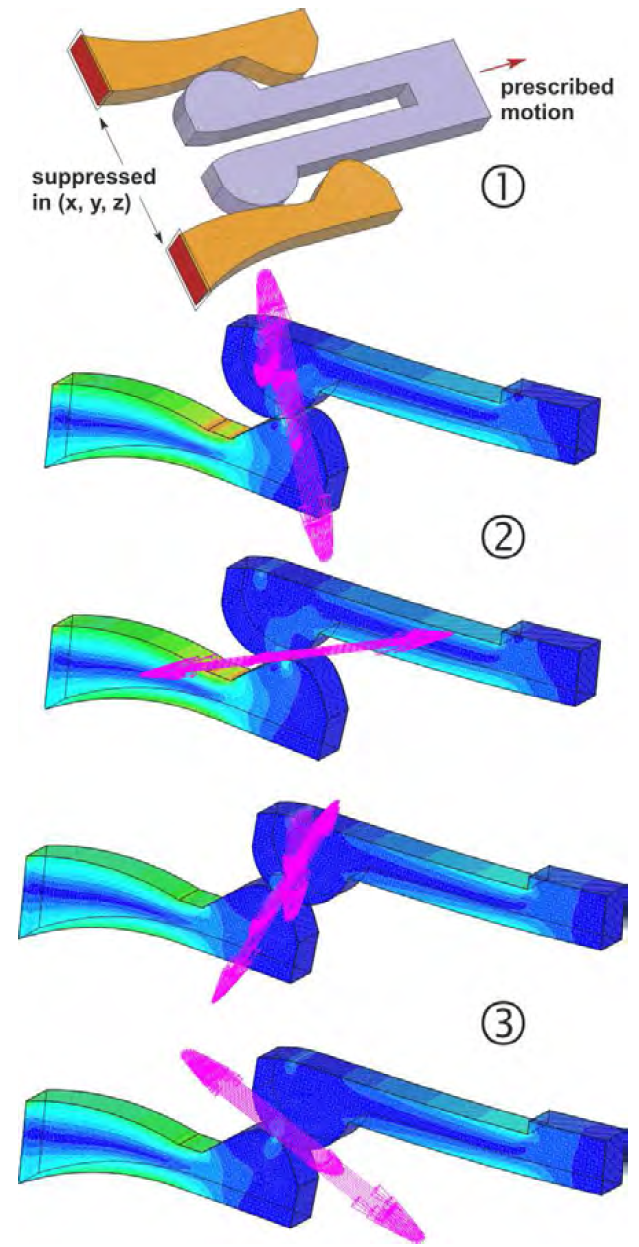
摩擦を伴う有限な相対すべり運動の事例。①はモデル概要、②と③はボトルネックに達する前後において、 節点応力分布に接触力およびせん断摩擦力ベクトルを順に重ね表示しています。
このモジュールでは、以下の特徴をサポートします:
- ・ この機能のための特別なモデリングを必要としません。接触曲面は更新プロセスにより変更されます。 そのため、接触情報は曲面(つまり、曲面-曲面もしくは曲面-節点の接触)で特定される必要があります。 なお、節点-節点接触、接地接触については、更新されません。
- ・ 有限すべり接触解析の機能は、摩擦ありおよびなしの両方で使用可能です。
- ・ 有限すべり接触解析の機能は、線形および非線形の両方で静的解析で使用可能です。
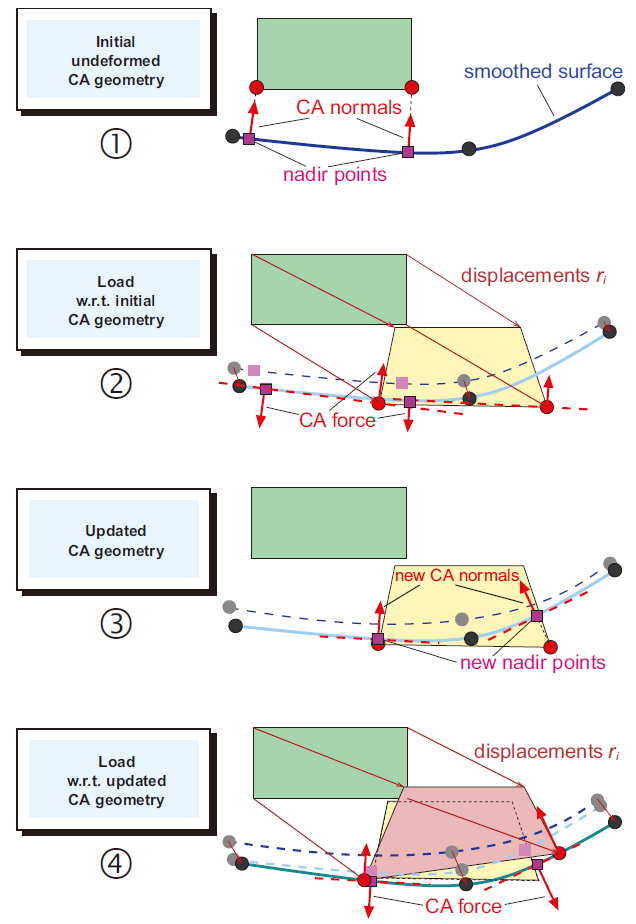
有限すべり接触解析における接触情報の更新は、概ね下図(PERMAS-NLS - 非線形静解析)で説明できます。 ステップ①では、典型的な微小すべりの範囲における接触過程を示しています。ステップ②と③では、 与えられた反復回数になるまで、もしくは設定された精度に達するまで、更新プロセスが繰り返し行われ、 ステップ④で更新された接触情報を満足する、2つの接触体の相対変位と接触力を結果として出力します。
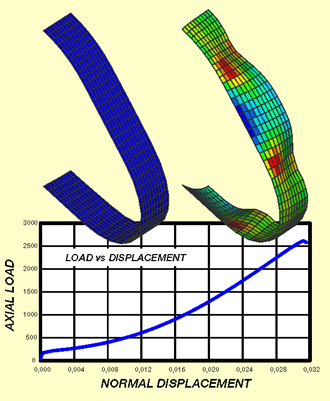
・ 幾何学的非線形
このモジュールは、幾何学的非線形解析の機能を含みます。ここでは、微小ひずみ条件下における大変形
(例えば、線形弾性材料挙動)が仮定されます。自動荷重ステップ制御機能に加えて、様々な非線形ソルバー
(Newton-Raphson法、修正Newton-Raphson法、割線Newton法、
ラインサーチ法、弧長法など)を利用することができます。
非線形特性はXYプロットで表現することもできます。このとき、荷重増分は自動でも手動でも指定できます。
・ 材料非線形
このモジュールは、次のような微小ひずみ条件下における非線形材料挙動の解析機能を含みます。:
- ・ 非線形弾性(Cauchy形式)
- ・ 塑性(von Mises、Tresca、Drucker-Prager、Mohr-Coulomb)
- ・ von Mises降伏基準に対するPowerLaw型の粘塑性
- ・ クリープ - 非線形弾性
- 塑性
ヤング率、降伏応力および応力-ひずみ曲線などの材料特性に対して温度依存性を定義できます。
さらに、クリープ計算では時間依存性が存在します。塑性に対する硬化則には、
等方硬化、移動硬化、混合硬化をそれぞれ定義できます。
シェル要素に材料非線形性を考慮するために、3次元のシェル定式化に基づく要素を使用できます。
この定式化は線形解析に対しても同様に用いることができます。
この要素(1次および2次の形状関数を持つ三角形および四角形要素)は、
既存のシェルモデルで非線形解析を行えるよう設計されました。
ガスケットのモデリングのために、ガスケット要素が利用可能です。
これらの要素は、実験から得られた実際のガスケットの荷重-変位曲線によって、
考慮すべき方向に対して非線形挙動を定義するために用います。
増分および反復ソルバーは、Newton-Raphson法、修正Newton-Raphson法、およびThomas法
をベースにしています。自動荷重ステップ制御機能によって、初期荷重ステップと全作用荷重
(または時間)の指定をオプションで行います。材料構成則は、テーブル形式またはユーザーサブルーチン
(FortranまたはC言語による)のいずれかを用いて定義できます。
慣性リリーフにも非線形材料挙動を考慮できます。
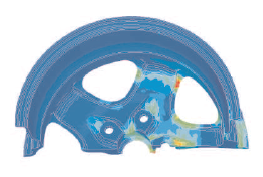
構造挙動は、鋳造、ロール圧延のような製造過程で生じるあらゆる初期条件の影響を受けます。
変位がゼロの状態でも、残留ひずみの結果を初期条件として用いることが可能です。
・ 材料非線形と幾何学的非線形の組み合わせ
材料非線形解析に幾何学的非線形の効果を考慮することもできます。圧力荷重のような追従荷重、温度荷重および慣性力を考慮できます。
・ 一般
接触定義は非線形解析に自動的に組み込まれ、非線形接触解析として実行されます。
非線形解析には、回転構造のような初期状態も考慮できます。
非線形解析の結果は、動的モード解析などの後続の解析で利用できます。
多くの場合、モデルの大部分は線形性を示します。これは、サブストラクチャリングを適用するための理想的な前提条件です。
ここで、線形部分をサブコンポーネントに、すべての非線形部分をトップコンポーネントに配置します。そうすることで、大幅な計算時間の短縮が見込めます。
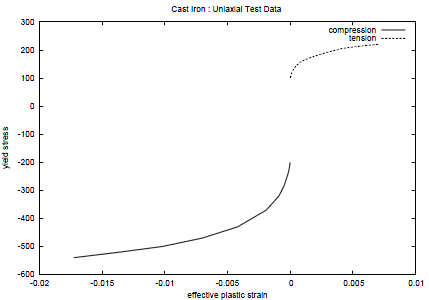
このモジュールは、NLSモジュールの標準の材料則を補完する形で、数種の材料則を追加提供します。:
- ・ 引張および圧縮で異なる挙動を考慮して、鋳鉄のための材料則を利用可能です。
- ・ さらに、非線形移動硬化 モデル(アームストロング-フレデリック法)により、繰返し負荷に対するモデルを定義できます。
PERMASが提供する材料構成則に加え、ユーザー定義の材料構成則を利用することができます。このために、材料則に沿った接線マトリクスとともに、 応力とひずみの計算を行うためのサブルーチンをユーザーが準備する必要があります。
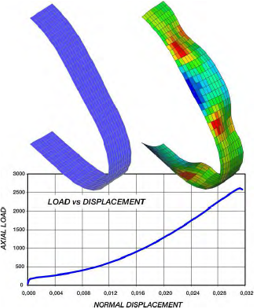
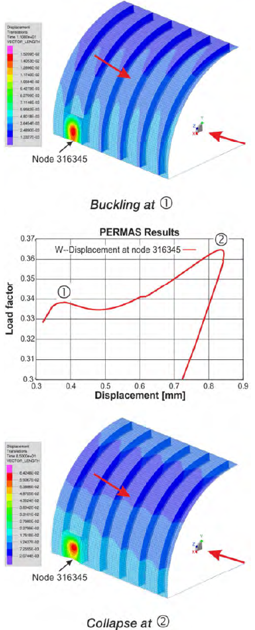
線形静解析に基づいて、座屈荷重係数と座屈モード形状を求めることができます。
モード寄与率の計算によって、座屈前挙動の非線形性の評価が可能です。
荷重係数とモード形状は、どのようなポストプロセッシングにも使用可能です。
PERMAS-DEV (動特性/固有値)モジュールは、構造物の実固有値およびモード形状を計算します(モード解析 )。 出力指定に対する、モード数と上限周波数の指定がサポートされます。PERMASには、大規模な固有値問題を解くことを可能にする、 非常に効率的なサブスペース反復アルゴリズムが実装されています。剛体モードは自動検出されるか、または明示的に指定した場合はサブスペース反復に先だち分離されます。
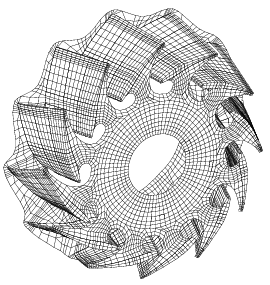
反対称境界条件における8次のモード形状
付加剛性効果を考慮した剛性マトリクスのアップデートが可能です。:
- ・ 任意の荷重に対する幾何剛性
- ・ 一定回転速度下における共回転基準座標系を参照する回転パーツに対する遠心力に起因する剛性
- ・ 一定回転速度下における慣性基準座標系を参照する回転パーツの対流剛性
- ・ 有効質量は、モーダルモデルの妥当性の指標として生成され、結果ファイルにプリント出力されます。
モード結果をさらに処理するための機能を利用することができます。:
- ・ モード変位からモード応力を計算できます。
- ・ さらに、モードひずみエネルギーおよびモード運動エネルギーの計算およびエクスポートが可能です。
- ・ モードの評価(例えば、局所モードまたは全体モードに関して)のために、構造に含まれる全セットに対するエネルギーバランスの計 算およびエクスポートが可能です。
- ・ MAC(Modal Assurance Criterion; モード信頼性評価基準)およびその他の係数により、2つの異なるモード解析のモードを比較 することができます。
- ・ 有効質量は、モーダルモデルの妥当性の指標として生成され、結果ファイルにプリント出力されます。
マルチボディシミュレーションプログラムに対して、弾性体を有限要素モデルとして組み込む場合、静的モード形状および非拘束振動モードを合わせて用いられることが頻繁に行われます。
単一コンポーネントモデルの場合、2組のベクトル(静的モード形状および動的固有ベクトル)が生成されます。これらのモードベクトルは、(例えばMBSシステムにおいて)直交化されていなければなりません。
しかしながら、大規模モデルを対象とする場合、このプロセスを実行するために膨大な時間が割かれます。時間の節約という見地から、この直交化の演算プロセスをPERMASの内部で行わせることができます。
PERMASにおいてモードベクトルの直交化を容易に行うための特別な工夫がなされています。
外部アプリケーションへの引渡しを目的とするモーダル空間におけるシステムマトリクスの生成が、一般化モーダル縮約によって可能です。モーダルモデルをエクスポートする方法は、
インターフェイスまたはマトリクスアイテム直接指定のいずれでも可能です。
このモジュールは、動的固有値解析に対する追加機能を提供します。:
- ・ 動的縮約
- ・ 複素固有値解析
- ・ 回転構造に対する回転速度に渡る固有振動数の計算
- ・ 動的縮約 Craig-Bampton法による動的縮約を提供します。この手法は、拘束振動モードおよび境界自由度に対する単位変位による静的たわみを利用して、サブストラクチャリングにおける動的縮約を担います。 Guyan縮約の場合と同様に、陽的な反復スキームによる驚異的なパフォーマンスが達成されます。
動的縮約機能の概要は次の通りです。:
- ・ サポートするソリューション - 動的構造解析
- 音響解析
- 流体-構造連成音響解析
流体-構造連成音響解析に対して、2つの縮約オプションが利用可能です。
- ・ "ドライ"境界面 - サブコンポーネントレベルにおける構造モードと音響モードの計算を分離します。
- 解析の全容は連成振動解析となります。
- 流体-構造の境界に縮約を適用できます。
- ・ "ウェット"境界面 - サブコンポーネントレベルにおける構造モードと音響モードの計算を分離します。
- 解析の全容は連成振動解析となります。
- 流体-構造の境界に縮約を適用できます。
- ・ 複素固有値解析 モーダル座標における複素固有値と複素固有ベクトルの計算を提供します。この方法は、事前の実固有値解析タスクの結果をもとに実行されます。
この解析による解析結果は次の通りです。:
- ・ 周波数
- ・ 複素固有値
- ・ 複素固有周波数(減衰係数および角周波数)
- ・ 等価粘性減衰比
- ・ 物理自由度およびモーダル自由度で得られる複素モード形状。複素モードのモーダル変位は、ベースとなる実モードのモード寄与率を表します。
対応するポストプロセッサ(MEDINAなど)により、複素モード形状の表示およびアニメーションが可能です。
- ・ 回転系の固有振動数 回転系の解析においては、いわゆるキャンベル線図の生成が頻繁に必要とされます。キャンベル線図は、固有振動数を回転速度に関係づけます。 キャンベル線図に必要となる各値は、1回の解析を実行するだけで自動的に生成されます。これらの値から、後続の周波数応答解析に興味のある、すべての周波数を選択することができます。
ASTRIUM Space Transportation社
(Les Mureaux)のご提供
DEVモジュールおよびDEVXモジュールによる固有値計算には、もう1つの方法があります。この方法は、流体-構造連成解析におけるモードの計算に利用できます。
多数のモードの計算を要する大規模モデルのように、実行経過時間が主にI/Oで決定される場合、この手法に大きなアドバンテージが生まれます。
モデル規模およびモード次数が増加すればするほど、MLDR法を用いることで得られるランタイムに対する恩恵はより大きなものとなります。
後続の動的応答解析において応答を計算する節点の数が少ない場合、実行時間に対する有益性はさらに増します。
その際に、固有値解析の結果として全体モード形状の生成を省略すれば、計算時間は飛躍的に節減されます。
MLDR法は、各パーツが既定の大きさを超えないよう自動分割することを基本としています。さらに、パーツ間のカップリングは可能な限り少なくする必要があります。
パーツの分割後、それらのパーツは動的縮約によりサブストラクチャとしてグループ化されます。
上記のプロセスは、1つのコンポーネントにより、完全なモデルが生成されるまで階層的に実施されます。コンポーネントには少数の節点と要素のみ残されており、
その動的挙動は、サブストラクチャから引き継がれるモードと周波数、さらに動的縮約の規則に従ってそれらが組み合わされることで決定されます。
このような過程を踏むことから、この手法を「多階層型動的縮退(Multi-Level
Dynamic Reduction: MLDR)と呼んでいます。
特定の節点および要素をメインコンポーネントに残しておく必要がある場合、ユーザーはそれらを明示的に指定することができます。
つまり、選択したモデルの部分をメインコンポーネントに含めることができ、後続のモード処理は残った小さなサイズのマトリクスで行うために、かなり効率的な計算となります。
この指定をすることにより、動的シミュレーション、MBSとの連携、残されたシステムの最適化、あるいは非線形性の考慮などが、非常に少ない計算時間で効率的に実行できるようになります。
この手法は完全に並列化計算に対応しており、マルチプロセッサシステムを利用すれば、さらに計算時間の短縮が可能です。結果的に、MLDRを使用することで、生産性は大きく向上するでしょう。
高精度な結果を得るためにモデルサイズを増大させ、より高次の周波レンジにおける動的シミュレーションが可能になります。
PERMAS-DRA (動的応答解析)モジュールでは、時間領域または周波数領域における構造応答の計算を実行できます。
動的運動方程式の求解は、物理座標に対して直接実行されるか、またはモーダル空間に変換した後、モーダル座標に対して実行されます。:
- ・ 時間領域の応答(過渡応答)は、運動方程式の時間積分により計算されます。
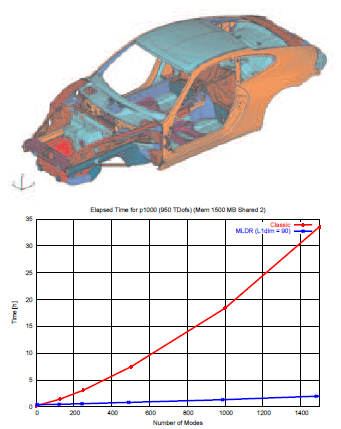
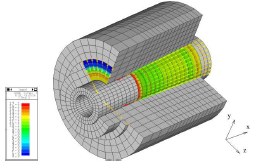
サブスペース反復法(上)とMLDR法(下)、(157412節点、164301要素(QUAD4)、944472自由度)
-
- 剛体運動の応答の有無にかかわらない絶対過渡応答
- 運動方程式の直接積分またはモーダル空間に変換後の積分。利用可能なソルバーはNewmark ß 法とHHT (Hilber-Hughes-Taylor)法です。
以下の要素により、局所的な非線形効果を考慮することができます。
-
- 非線形バネ要素
- 非線形ダンパー要素
- 流体-構造の境界に縮約を適用できます。
- ・ 周波数領域の応答(周波数応答)は、線形の複素連立方程式を加振周波数ごとに解くことで求められます。
- 剛体運動の応答の有無にかかわらない絶対周波数応答
- 連立方程式の直接求解、またはモーダル空間に変換後の求解
- ・ 過渡的な現象を直接解析することなく、定常応答の計算が可能です。そのために、いくつかの周波数応答解を時間領域で重ね合わせます。
さらに、静的な荷重ケースを考慮することで、既知の調和成分からなるすべての周期的な加振に対して更に精度の高い重ね合わせを行います。
節点セットを指定して出力結果の要求をセットのメンバーだけに限定することで、モードの重ね合わせ処理における実行時間とディスク容量を大幅に削減できます。
以下の機能は、過渡応答解析および周波数応答解析の両方で利用可能です。:
- ・ 減衰特性は、次のいずれかの方法でモデル化できます。:
- p要素に対する材料減衰または構造減衰
- コンポーネントに対する全体構造減衰
- 比例減衰(Rayleigh減衰)
- 粘性ダンパー要素
- モーダル粘性減衰
- モーダル構造減衰
- モーダル構造減衰および比例減衰
- モーダル減衰マトリクスの直接入力
- 減衰マトリクスの直接入力
周波数領域の計算では、構造減衰は周波数の関数としても定義できます。
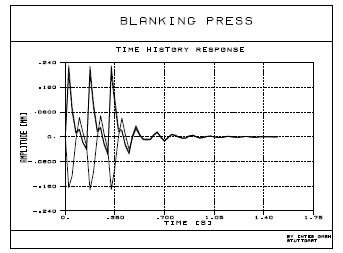
- ・ 加振は、時間または周波数の関数として静的荷重ケースで定義されます。荷重定義には次のものが利用可能です。: - 集中荷重(力またはモーメト)
- 分布荷重(線、面または体積に対する荷重)
- 慣性力
- 強制変位
- ・ まず、一次結果は以下を求めます。: - 変位
- 速度
- 加速度
これらは時間または周波数の関数として出力され、XYプロット表示できます。
- ・ さらに、二次結果は以下を要求できます。: - 反力
- 応力および合応力
- ひずみエネルギー
- 運動エネルギー
- 音響放射パワー密度
モード法を使用した場合、次の機能を利用できます。:
静的モード形状:動的モードからなるモーダル基底を拡張します。これには次の2つの利点があります。:
- ・ 低次周波数レンジにおける結果の精度を根本的に改善します。
- ・ コントロール要素の内部状態変数など、非構造自由度を考慮できるようになります。
静的モード形状は、次のいずれかによって指定し、得ることが可能です。:
- ・ 節点変位の直接指定
- ・ 外部荷重の指定
- ・ 別の解析結果の指定
- ・ 指定した要素の自然負荷(バネ力など)の指定
- ・ コントロール要素の内部自由度の指定
アセンブリシチュエーション:多くの荷重ケースを有す周波数応答解析を飛躍的に高速化できます。 すべての動的荷重ケースをそれぞれ解く代わりに、合成された応答解析を1回だけ実行しそれぞれの解を求めます。
モード結果を処理するための機能をさらに利用することが可能です。:
- ・ 構造応答の評価のために、一次結果のモード寄与率の計算およびエクスポートが可能です。
- ・ 構造応答に対する単一自由度の寄与度を評価するために、節点のモード寄与係数の計算およびエクスポートが可能です。
- ・ 過渡応答解析では、時間領域に渡る応力または要素力の最大値および実効値による統計的な評価を行うことができます。これらの統計量は、例えば、耐久性の検討に利用できます。
このモジュールは、構造応答解析に対する追加機能を提供します。:
- ・ スペクトル応答解析(地震動スペクトル応答解析)
- ・ ランダム応答解析(パワーススペクトル密度(PSD)解析 )
- ・ スペクトル応答解析 地震解析のようなベース加振の場合、動的応答挙動は特別な手法で求め、応答の最大値を得ます。この手法では、次の要件が満たされなければなりません。:
- ・ 単一方向かつ並進運動によるベース加振
- ・ 他の荷重はなし
- ・ 解析はモーダル空間に対してのみ行います
- ・ モーダル粘性減衰のみ
-
ベース加振の方向を指定した後、荷重が時刻歴加振のスペクトル(応答スペクトル)によって定義されます。その後、解析は次のように実施されます。:
- ・ 興味のある最大周波数まですべての動的モードを計算
- ・ 最大モード寄与を計算
- ・ 7つの総和規則(CQCや10%ルールなど)の1つにより最大モード寄与の総和を計算
- ・ ピーク値のエクスポートまたはプリント出力
- ・ ランダム応答解析 悪路を走行する車、風荷重下にある建物、あるいは荒れた海上の船などでは、加振は多くの場合予測不能です。
そのような確率論的な荷重は、ランダム過程によって記述することができます。このようなプロセス間の相関関係とそれらの周波数領域への変換が、パワースペクトル密度(PSD:Power Spectral Density)の主要なコンセプトとなっています。
特別な現象のひとつはホワイトノイズです。ホワイトノイズは、全周波数範囲に渡って一定のパワースペクトル密度を示します。 荷重はパワースペクトル密度として指定され、結果もRMS量およびPSD(パワースペクトル密度)として計算されます。
この手法は、モード法として実装されており、固有値解析の実行がファーストステップであり、続いてモーダル空間において応答解析が実行され、後続の処理として物理空間への逆変換を経て、 結果のエクスポートおよびポストプロセッシングへと繋がります。
PERMAS-FS(流体-構造連成音響解析)モジュールでは、音響モードの計算を実行できます。同様に、流体-構造連成システムの固有値および周波数領域または時間領域における連成または非連成応答の計算を実行できます。
この計算は、直接法またはモード法のどちにも対応しています。
流体は圧縮性および非圧縮性のどちらも許容します。非連成の計算では、流体の吸収特性および減衰特性のすべてが利用できます。流体の減衰値は周波数依存特性としての適用が可能です。

Chantiers de l'Atlantique社(Saint-Nazaire)ご提供
様々な特殊機能により境界条件をモデル化できます。:
- ・ 表面波は特別な要素によりモデル化されます。
- ・ 流体と構造の境界のモデルとして、特別な連成要素が実装されています。また、これらの要素を使用することで表面吸収をモデル化することもできます。 さらに、音響減衰を定義するもうひとつの方法は、体積ダンパー(車のシートなど)を用いることです。
- ・ 半無限境界要素により、無限空間を取り扱うことができます。
- ・ 放射境界条件(RBC)を特別な要素によりモデル化することができます。これらの要素は、Bayliss-Turkel理論とEngquist-Madya理論に従います。
上記の連成要素における面の法線は、流体から構造へ向かう方向でなければなりません。この条件は自動でチェックされ、流体と構造を連成させる際に生じる矛盾や誤りの原因を事前に排除します。
動的モード周波数の計算において、完全な連成モードと流体の付加質量によって更新される構造モードとの間には、以下のような違いがあります。:
- ・ 連成構造における実固有値およびモード形状の計算は、ベクトル反復法により同時に実行されます。ここで、出力に関してモード数および上限周波数の指定がサポートされています。 使用するアルゴリズムの特別な定式化は、非常に大規模な固有値問題も効率的に解くことが可能です。
- ・ 付加質量の問題は、構造解析のための実固有値解析用ソルバーで解くことができます。この際、構造モードの計算に流体の質量が加味されます。
数多くのモードを求める必要があり、かつ大規模モデルを対象とする連成固有値計算を解く場合に、MLDRを用いることで実行時間を大幅に節減できます。
動的応答挙動の計算に対して、次の手法を利用することができます。:
- ・ 時間領域の応答(過渡応答)は、運動方程式をモード法により解くことで求められます。求解には、Newmark ß法およびHHT(Hilber-Hughes-Taylor)法を利用できます。
- ・ 周波数領域の応答(周波数応答)は、指定した加振周波数ごとに線形の複素連立方程式をモード法または直接法で解くことで求められます。 一般に、完全に密な連立方程式を解かなければなりません。モーダル空間における計算の場合、反復法ソルバーを使用することで、計算を高速化できます。
節点セットや要素セットを指定して、そのセットに対してのみ結果を計算することで、モード重ね合わせにおける実行時間を大幅に低減することが可能です。またこのとき、応答結果を限定するのでディスク容量も大幅に削減されます。
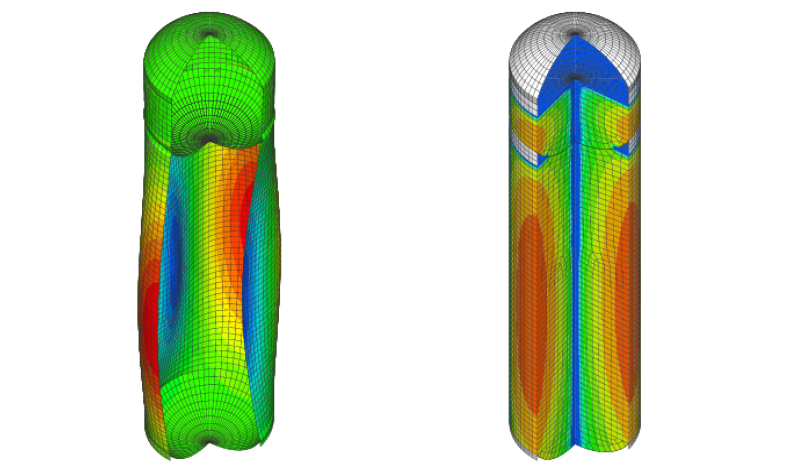
連成振動モード(左)と対応する圧力のモード(右)
減衰を次のように定義することができます。:
- ・ 構造に対して: - 要素に対する材料減衰または構造減衰。また、必要に応じて周波数依存性の減衰を定義できます。
- ・ 流体に対して: - 境界面の吸収
- ・ 連成システムに対して: - モーダル粘性減衰(連成システム)
- 体積吸収、また、周波数依存性の減衰を定義できます。
加振は、周波数の関数として静的荷重ケースで定義することができます。荷重定義には次のものを利用することができます。:
- ・ モジュールの節に記載した構造荷重
- ・ 強制圧力
一次結果として次の量が計算されます。:
- ・ 変位
- ・ 圧力
- ・ 速度
- ・ 加速度
上記のデータは、XYプロットの表示のために時間または周波数の関数として出力されます。さらに、次の結果を要求することができます。:
- ・ 反力
- ・ 応力および合応力
- ・ ひずみエネルギー
- ・ 運動エネルギー
- ・ 音響放射パワー密度
- ・ 粒子速度
このモジュールでは、非線形性を含む構造解析を実行することができます。:
- ・ クリープ、非線形弾性、塑性および粘塑性のような材料非線形性
- ・ 非線形バネまたはガスケット要素、さらにコントロール要素のような非線形要素
- ・ MPCの更新を伴う(不整合メッシュ間)弾性体の大変位運動
現バージョンでは、幾何学的非線形効果および接触の考慮はできません。
時間積分は、Newmark法または一般化α法により行われます。後者の手法では、数値的に減衰効果を含めることで積分スキームを安定化させています。
Newton-Raphson法や修正Newton-Raphson法のような直接解法を利用することができます。自動時間ステップ制御機能により、時間ステップは常に適切な値として設定されます。
非線形動的解析を実行する前に、サブストラクチャリングおよび動的縮約により、完全な弾性挙動を示す部分だけを縮約することができます。
PERMAS-HTおよびPERMAS-NLHT(次節)により、温度場の解析を実行することができます。
- ・ 温度場は定常または過渡の両方を定義できます。
- ・ 熱伝導と熱容量を、非線形材料データとしてテーブル形式で入力することができます。
- ・ 温度および空間依存の熱伝達係数は、関数による一般的な方法で定義できます。
PERMAS-HTでは、表面熱伝達をモデル化するために必要な熱伝達要素すべてを提供します。さらに、それらの要素では、表面から熱が流入/流出する要素の表面積を求めることもできます。
オプションで、熱伝達要素にフィルム厚を定義することができます。フィルム厚により、過渡解析において境界層の熱容量をモデル化することができます。
静解析で利用可能な要素はすべて熱伝導解析でも利用することができます。シェル要素を使用する場合、上面と下面に生じる温度勾配を指定することもできます。
熱応力問題の連成解析は完全に自動化されています。そこでは、変位、ひずみおよび応力が温度場結果を直接用いて計算されます。静解析で用いられる材料データ(弾性係数および熱膨張係数)に温度依存性を定義します。
さらに、PERMAS-CCLモジュールを用いることで、CFD解析から熱伝達境界条件を取り込めます。また、それぞれの完全な連成解析を実行することも可能です。
事前の解析結果を用いた過渡解析を実行することができます。完全な熱荷重サイクルのシミュレーションを実行する際には、周辺条件の瞬間的な変化も簡単に表現できます。
伝熱問題に対して固有値と固有モードを計算するモード解析を行うことができます。
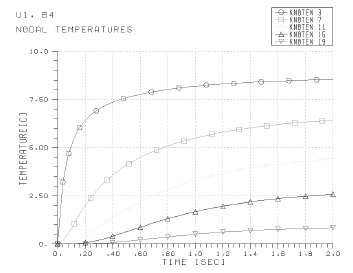
次の熱荷重および境界条件が利用可能です。:
- ・ 定常的な熱荷重として、点熱流および線、面および体積に対する分布熱流束を定義できます。
- ・ 過渡的な熱荷重として、定常的な熱荷重パターンを時間の関数と組み合わせて容易に定義できます。
- ・ 温度固定境界条件および熱伝達要素に対する周辺温度も定義できます。
熱伝導解析における一次結果は温度場と熱流束となります。要求に応じてさらに次の結果を計算させることができます。:
- ・ 温度場の勾配
- ・ 任意の内部面を通る熱流束
- ・ 絶対値または面積当たりの値である熱流を、任意の要素セットの指定により、表面の一部を通る熱流として出力することができます。
さらに、過渡解析では、一次結果および一次結果より導かれる結果を任意の点に対して出力することができます。これらの結果からXYプロットを生成できます。
PERMAS-HTモジュールでも非線形解析を実行することはできますが、このモジュールはさらに高度なアルゴリズムを提供しており、より非線形性の強い定常および過渡的問題を解くことができます。
前節の記述とは反対に、自動ステップ時間制御アルゴリズムが定常解析および過渡解析に対してともに用いられます。自動時間ステップ制御機能は、ステップ点を明示的に指定することもできます。その際の指定は時間または荷重レベルで行います。
荷重ステップおよび特定の時間ステップを明示的に定義することで、結果出力点の選択を行えます。
- ・ 輻射熱交換 輻射による熱伝導は、温度の上昇に伴ってその重要性を増します。また、ブレーキ、燃焼エンジンおよび冷却素子など、空洞や自己遮蔽効果を考慮すべき部品に対する解析でも重要です。 その場合、熱伝達と輻射熱を考慮した熱伝導の解析が必要です。
この機能を使用するためには、面間の熱交換(ボディ内部からの輻射熱は考慮しない)、灰色体からの輻射熱(波長に依存しない輻射熱)および拡散輻射(輻射方向に依存しない輻射)という仮定が前提となります。
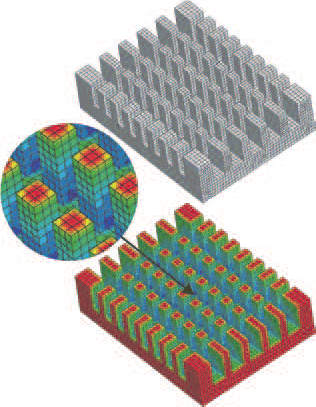
輻射の計算における特徴は以下のとおりです。:
- ・ 輻射は熱伝導解析の一部として用意されています。
- ・ 熱伝達要素により、輻射面をモデル化することができます。ここでは、輻射を考慮すべきすべての面要素は、熱伝達要素でモデル化されなければなりません。
- ・ 形態係数は面要素に渡る直接積分で計算されます(平均値を計算しません)。
- ・ 膨大な数の面要素を含むモデルの形態係数の計算スピードの高速化のために、粗大化を自動的(または選択的)に行い、面要素の数を低減します。
- ・ 並列化計算機能により、さらなる計算効率を得ることができます。
- ・ 輻射境界条件を考慮した非線形伝熱方程式が組み込まれた連成問題は、数回の反復ステップを通して実行されます。これは定常解析および過渡解析いずれでも同様です。
ホワイトボディの周波数応答最適化
(上図形状および寸法パラメータを用いたもご参照のこと)
純粋なFEモデリングに加えて、PERMASには設計モデルの定義およびその自動最適化の機能が搭載されています。
輻射の計算における特徴は以下のとおりです。:
- ・寸法最適化: - ビーム要素の断面積、断面2次モーメント、およびこれら特性値間に定義する一般関数
- 標準ビーム断面に用意されたすべてのパラメータ
- 膜要素およびシェル要素の厚み/オフセット/非構造質量
- バネ要素の剛性と質量
- 質量要素の質量
- 減衰要素の減衰パラメータ
- コントロール要素のパラメータ
- 熱伝達係数
- 材料パラメータ
- ・形状最適化: - 節点座標
- 設計要素の利用
- ビードデザイン
- ・設計変数のリンク
前述の最適化において、設計変数の変更が可能な限界値を定めることができます。次の解析結果値に対しても、事前に限界値を設定することが可能です。:
- ・ 変位、速度、加速度
- ・ 要素力
- ・ 反力
- ・ 応力
- ・ コンプライアンス
- ・ 重力
- ・ 接触問題におけるギャップ量
- ・ 接触圧
- ・ 接触反力
- ・ 固有周波数
- ・ 音響放射パワー密度
- ・ 温度
- ・ 一般的な拘束
上記の結果量の組み合わせまたは任意の関数として与えることができます。定義関数として、max/min、absmax/absmin、またはRMSのような数学上の基本的な関数が用意されています。
重量または任意の拘束条件は、最適化の目的関数として利用できます。
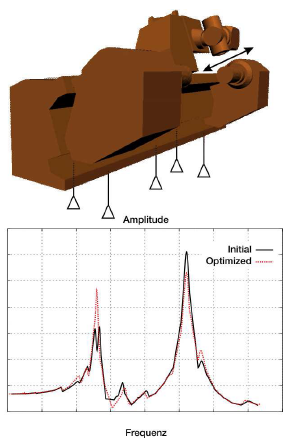
従属節点に対しても形状変更を適用できます。つまり、構造を再度メッシングすることなく、不整合メッシュを積極的に活用した大まかな形状変更が簡単に行えるようになります(下図工作機械の周波数応答の最適化例をご参照)。
現在、設計最適化モジュールは、次の解析タイプで利用可能です。:
- ・ 線形静解析
- ・ 接触解析
- ・ 慣性リリーフ
- ・ 非線形材料挙動
- ・ 固有値解析
- ・ モーダル周波数応答解析
- ・ 定常熱伝導解析
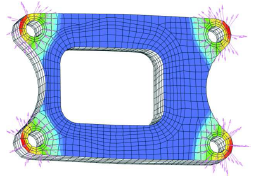
機械本体と基礎バネ要素の最適配置問題
目的関数は、機械の中心点の最大柔性として設定
周波数応答に対して最適化を適用する場合、設計拘束条件および目的関数として、上記に挙げた振幅、位相、実部、虚部を定義できます。また、設計拘束条件に対する限界値に周波数依存性も考慮できます。
異なる解析タイプをたった1回の最適化タスクに含めることができます。同様に、寸法および形状パラメータを複合することが可能です。
最適化に複数の荷重ケースを考慮することができます。同様に、バリアント解析の要領で異なる境界条件を考慮することもできます。さらに、動的モード周波数にも最適化を適用できます。周波数応答の最適化では、
構造変更が行われるたびにモードトラッキングが自動で実行されます。
最適化を適用した部分が全体構造のごく一部である場合、トップコンポーネントに設計空間を分離してサブストラクチャリングを実行すれば、
実行時間の大幅な削減に繋がります。変更の必要がない部分についての縮約プロセスは最初の1回目だけ行われます。
最適化計算後、目的関数の履歴および各反復ステップにおける設計の妥当性が傾向として得られます。
さらに、設計変数および設計拘束の値は、それらを得た反復の回数に対する関数となります。これらの関数はXYプロットとして容易に視覚化できます。また、感度をファイルにエクスポートすることもできます。
さらに、要素プロパティを結果処理(例えば、厚みの分布)のために用意することや、またポストプロセッシングのためにエクスポートすることもできます。
形状最適化の結果は、変位結果として最適化前のモデルとともに出力されるか、または最適化された座標値を持つ同一トポロジーの新しいモデルとして出力することができます。これらはポストプロセッシングに利用できます。
ロバスト最適設計は、信頼性拘束条件を追加することによって行えます。ここで導かれる最適化設計は、上記のすべての設計拘束条件を満たし、かつ不確実であったモデルパラメータに関しても信頼性を得たものとなります。
トポロジー最適化(位相最適化)は、モデル空間のある部分に対して、ユーザー定義の基準を参照して、最適かつ設定した一連の条件を満足するような有限要素構造を検出するための手法です。
このタスクにおいて、対称構造となるモデルの一部(設計空間)は、有限要素で充填されていなければなりません。有限要素はそれぞれ設計変数(充填率;0~1の値)を有しています。
充填率は、要素剛性に対するスケールファクターの計算に用いられます。充填率がゼロに近い値を取るとき、剛性もゼロに近い値を取ります。
そして、残りの有限要素は力学的挙動になんら寄与しないため、無視することができます。一方、要素の充填率が高い場合、与えた基準を満たすことが必要となります。
この過程で検出されたレイアウトは、設計空間に含まれる要素のサブセットで構成されることは明らかです。設計空間を細かく離散化すればするほど、結果として得られるレイアウトは詳細なものとなります。
一方で、設計空間を細かく設定すれば計算負荷も増大します。
完全に統合されたトポロジー最適化機能を提供することで、開発の構想段階を全面的にバックアップします。:
- ・ 設計空間に対する可変/固定部分の指定
- ・ 境界条件の指定
- ・ 荷重の指定
- ・ 残留体積の目標定義
- ・ 最適化に対する設計拘束条件の追加
モデリングは連続体要素(膜要素、シェル要素およびソリッド要素など)により行われ、さらにサブストラクチャリングもサポートされます。 レイアウト最適化機能における追加のモデリングパラメータは次のとおりです。:
- ・ 固定/可変の設計要素: - 設計要素ごとの充填率
- 設計変数の限界
- 設計変数の変更限界
- ・ 製造環境による拘束条件: - 開放方向:
鋳物を想定した特別な設計拘束条件を指定する必要があります。この拘束は、トポロジー最適化の結果を生成可能なものとするために適用されます。 開放方向は、この種の製造環境による拘束条件を制御するために指定されます(下図レイアウト最適化例をご参照)。加えて、閉構造(ハウジングなど)を得るために、残留部材肉厚の最小値を指定できます。 開放方向を反対に指定する場合、固定モールド分割線を指定することができます。
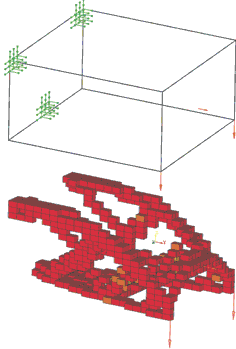
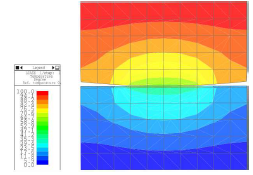
境界条件と荷重が与えられた設計空間(上)と最適な材料分布(下)
-
- 対称条件:
面対称、軸対称および周期対称といった各対称条件を指定することで、レイアウト結果の最終的な特性を決定できます。
- 繰り返し構造:
構造中の異なる部分に対して同じレイアウトを適用したい場合、設計要素間にリンクを設定することができます。
- 最大部材サイズ:
最大部材サイズにより、構造に残す部材の厚さを制限することができます。この指定は、開放方向のオプションです。
- 最小部材サイズ:
構造に残す最小部材寸法(例えば、幅や厚み)は、対応するパラメータ(チェス盤フィルターと呼ばれます)により制御できます。
- ・ 設計拘束および設計目的: - コンプライアンス
- 重量
- 反力
- 固有周波数(モード範囲)
- 変位
- 加速度、速度
- (非設計空間における)応力
- (非設計空間における)要素力
- (非設計空間における)音響放射パワー密度
設計拘束はそれぞれ、目的関数として使用することもできます。
上記に挙げた基本的な設計拘束条件を用いて、関数としてより複雑な条件も構築できます。
一般的な目的関数の機能の範囲で、複数の拘束値に依存する目的関数
(max/min、absmax/absmin、RMSなど)を設定することができます。
- ・ マルチモデリング - 様々な重ね合わせオプションによる複数荷重ケースの同時考慮
- 様々な設計バリアントの適用
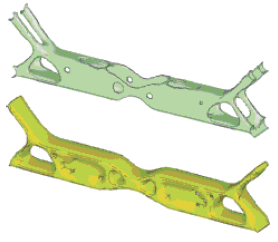
方向を指定しない場合(上)
指定した場合(下)
レイアウト最適化は、多くの解析タイプをサポートしています。:
- ・ 線形静解析
- ・ 接触解析
- ・ 動的固有値解析
- ・ モーダル周波数応答解析
トポロジー最適化を行っていると、固有周波数とモード形状は大きく変動します。そのため、局部モードを抑制するための戦略を設定すべきであり、それは特に重要となります。
最適化計算自体は、下記のアルゴリズムの1つを用い実行されます。:
- ・ GCA (Global Approximation)
固有周波数および静的および動的設計拘束の組み合わせに対応します。 - ・ PD (Primal-Dual Solution)
最適化の反復計算の制御は、目的関数の収束基準または最大反復数のいずれかで行います。
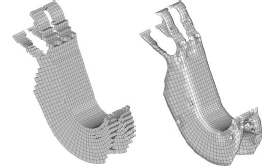
一次結果(左)、スムージングされた面(右)
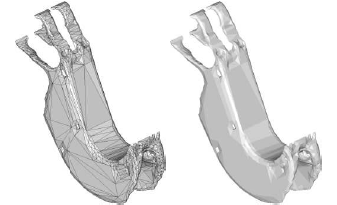
三角形メッシュ(左)、サーフェスのグラフィック表示(右)
レイアウト最適化の結果として、目的関数の履歴に加えて要素の充填率が提供されます。充填率に基づいて計算された構造は、ポストプロセッサで容易に視覚化することができます。
残った構造領域には、さらに次のような処理を加えることができます。:
- ・ 外殻モデルの生成: 充填率(自動決定された値または指定値)に対して生成された構造表面が、四角形および三角形のメッシュとして抽出されます。
- ・ スムージング: パーツ境界、荷重および運動学的拘束を考慮して外殻モデルがスムージングされます。
- ・ 多角形縮小: サーフェスの表示容量を可能な限り小さくするために、外殻モデルメッシュから微小な三角形および四角形が取り除かれます。
- ・ エクスポート: 残った三角形メッシュは、FEメッシュとしてエクスポートし、ポストプロセッシングに使用することができます。
- ・ リメッシング: トポロジー最適化の計算結果から得られた外郭モデルを用いて、VisPERが内蔵するテトラメッシャーによりリメッシングを行うことが可能です。
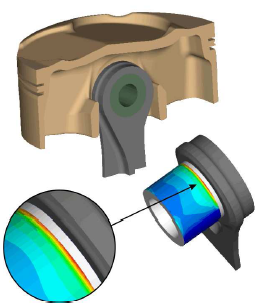
(Mahle社ご提供)
上図はパーツ間に生じたエッジ圧を示しています。
(最適化結果については、(上図ピストン-ピストンピン間の接触圧の最適化例ご参照)
このモジュールでは、PERMASの適用範囲を根本的に拡張する最適化ソルバーを利用することができます。本モジュールによる拡張として、次のものが挙げられます。:
- ・ 新しい局所法に基づく信頼領域により、アダプティブステップサイズ制御機能が実装されました。これにより、すでにPERMASに搭載されているユーザー定義の静的な変更限界を拡張します。
- ・ 信頼領域法では、最良の点の動向を保持します。点を破棄することでは何も達成されません。本手法による拡張機能は、任意の新しい点を適用するところにあります。
- ・ 微分量を用いない最適化および大域的最適化のための新しい手法が利用可能です。
上記の手法を用いることで、PERMASの最適化の適用範囲に新たな領域が開かれます。例えば、接触解析および非線形材料解析に最適化を適用できます。
新しい局所的手法を利用可能です。この手法は次の微分量ベースの手法を含みます。:
- ・ SQP(逐次的2次計画法; Sequential Quadratic Programming): この手法は、ダンプされたNewton法に有効制約法を組み合わせ、最適化問題の方程式へ適用した手法です。 本手法は最も汎用性の高い手法(しかし、必ずしも構造力学に必要であるわけではありません)です。BFGS法に基づく更新により、2次の情報を利用することができます。
- ・ SLP(逐次的線形計画法; Sequential Linear Programming): この手法は、線形近似可能であるときのみに用いられます。通常は、2次の情報が欠落するためにSQPよりも低速な手法となります。 しかし、場合によっては微分量ベースの手法よりもロバスト性の高いものとなります(例えば、ある量が急激な勾配を示すような場合)。
- ・ SCP(逐次的凸計画法; Sequential Convex Programming): 通常は、構造力学に基づく古典的最適化問題に対する最も優れたアルゴリズムに基づく手法となります。 OPTモジュールでは、最適化手法としてこのSCPと同じタイプの手法を使用しています。
万が一、微分量を利用することができないような場合(例えば、接触問題や非線形材料挙動を対象にする場合)、または微分量の計算精度が十分ではないとき(周波数応答解析など)、 微分量を用いない手法の適応が有効です。新しく開発された微分量を用いない(局所的)手法では、次のようなアプローチが用いられます。:
- ・ 有限差分を使用した微分量ベースの手法(SQP、SLP、SCP)の適用。用いる関数は十分に滑らかでなければなりませんが、ある区間における有限差分パラメータの選択は問題とはなりません。
- ・ 微分量を用いない手法WLIN(くさび形拘束線形近似; Wedge constraint LINear approximation)により、有限差分パラメータを選択する必要は無くなります。この手法は煩雑な問題に用いられます。
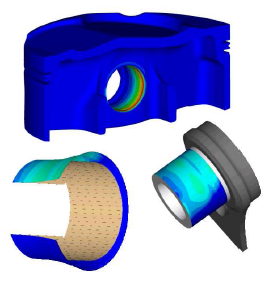
(Mahle社ご提供)
上図はピストンの最適化形状 および低減されたエッジ圧を示しています
全域的に最小値を検出する必要がある場合、局所的手法に頼ることは多くの場合、適切とは言えません。そのような全域的な最適化問題に対しては、次のアプローチを利用すべきです。:
- ・ Multi-Start法(MS)およびランダムポイント法により、最小値を局所化するために微分量ベースの手法を用いることができます。 この手法は最良な点の動向を保持するためにも適用されます。このアプローチは自動化された試験手法としても知られています。ループの最大数を指定して計算を停止させることができます。
- ・ もうひとつの手法としてLDR(局所的に修正された矩形分割:Locally improved variant of the Dividing Rectangles
(DiRect))が用意されています。
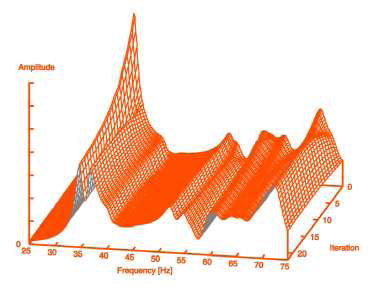
下図(LDR法によるばね-ダンパーシステムの大域的最適化例)にはこのアプローチを用いた一例を示しています。この手法では、拘束問題に適応するため一般化され、局所的な部分問題を解くことで改善を果たしています。
ここで、設計空間内の重要な点列を生成することで、大域的な解の近似を保証しています。
この手法は低速な手法であり、小規模なモデルへの適用のみ有効です。したがって、使用の際には、モデル縮約を行うことを強く推奨します。
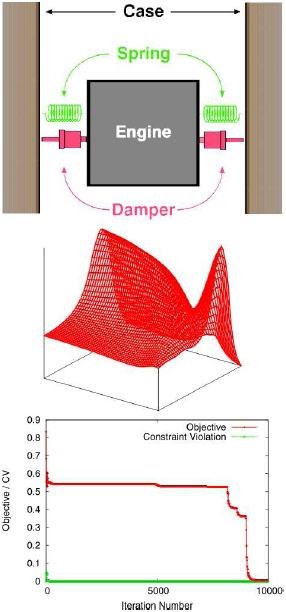
4つの設計バリアント(上)、2つの設計変数を拘束し、 また2つの設計変数を目的関数とした場合の最適解(中)、 目的関数の履歴および反復中の拘束違反(下)
設計モデルに様々な荷重条件を与え、その挙動を予測する従来のアプローチでは、モデルとして決定論的なモデルが用いられます。
そのような解析で得られる結果は、安全マージンを考慮した最大応力または最大変位のような典型的な制限拘束と比較され、評価が行われます。
このような過程は構造安全性問題に対する決定論的アプローチと呼ばれ、有限要素法は決定論的アプローチを達成するための広く認められたツールとなっています。
決定論的アプローチとは対照的なものとして、確率論的解析による設計が挙げられます。ここでは、構造特性のいくつかまたは荷重が、確率分布特性のみが既知である不確実な変数と仮定されます。
この設計法における設計拘束の限界値は、通常、決定論的アプローチと同種のものとなります。しかし、確率論的解析から得られる結果は、上記の拘束限界値に対する違反の確率およびモデルの不確実な特性に対する確率の感度を導きます。
このモジュールでは、有限要素解析とRCP社(ミュンヘン)開発の確立されたコードであるCOMRELプログラムを組み合わせた機能が提供されます。つまり、両ソフトウェアシステムに蓄積されたノウハウを単一のアプリケーションに統合しながら、
確率論的有限要素法アプローチの簡素化を達成しています。:
次の3ステップで信頼性解析は構成されます。:
- ・ 構造解析における不確定量(形状パラメータまたは荷重パラメータ)の分布関数を割り当てた基本変数による定義
- ・ 構造解析における結果量に関連する限界状態関数(または違反関数)の定義
- ・ 限界状態関数ごとの失敗確率の計算
基本変数として次の量を使用できます。:
- ・ (形状データまたは座標のような)設計パラメータ
- ・ 荷重係数
- ・ 材料パラメータ
- ・ 限界状態関数のパラメータ
- ・ その他の基本変数パラメータ
20以上の異なるタイプの分布関数を利用して、不確定基本変数を記述することができます。
確率論的解析では、次の解析タイプに対して違反パラメータの検査を行うことができます。:
- ・ 線形静解析
- ・ 接触解析
- ・ 動的固有値解析
- ・ 周波数応答解析
多様な解析に対応して、数多くの手法を利用することができます。:
- ・ 1次/2次信頼性手法(FORM/SORM)に基づく効率的な感度解析法
- ・ 応答曲面法
- ・ アダプティブサンプリングを用いたモンテカルロシミュレーション
- ・ 入門的モンテカルロシミュレーション
信頼性解析では、複数の荷重ケースを定義することができます。同様に、異なる違反関数を持たせることで複数の境界条件を考慮することもできます。
- ・ 違反関数の定義には、次のものを利用できます。: - 一般的な関数
- 次の量に対する依存関係として
* 結果(変位、応力など)
* 基本変数
* 定数
- ・ 信頼性解析における一次結果は次のとおりです。: - 限界状態関数ごとの違反確率
- 限界状態関数のパラメータ感度
- 基本変数に対する結果の感度
- モンテカルロシミュレーションに対する各反復の選択データ
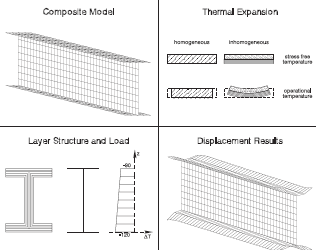
積層材解析モジュールLAでは、多積層の繊維強化複合材のモデリングおよび解析を行うことができます。積層材解析のために、PERMASは3節点および4節点シェル要素を提供します。
積層材の材料設定は、形状、境界条件および荷重と同様に、MEDINAやI-DEASなどのプリプロセッサを用いずに行われます。
ABDマトリクスの形成は、層数および並列、また各層に対する厚み、繊維方向および材料特性を用いて一般的な方法に従って行われます。
各層の応力およびひずみは、解析の結果得られる要素力から導出されます。
MEDINAをポストプロセッサとして用いれば、破壊基準、破壊インデックスおよび安全係数を評価することもできます。加えて、複合材構造に対しても、その他すべてのポストプロセッシング機能を利用できます。
このモジュールでは、定常電磁場解析の機能を提供します。磁場解析は、事前の計算による定常電流分布に基づいて実行されます。この電磁場解析では、電場に対してスカラーポテンシャル、そして磁場に対してベクトルポテンシャルが用いられます。
様々な荷重タイプがサポートされています。
特異性に関して、その検出および取り扱いは静解析の場合と同様にして行われます。
電場から誘起されたジュール熱を後続の熱解析に引き継ぐことができます。さらにジュール熱を用い後続の静解析を実行することにより、熱応力を計算することもできます。
磁場から誘起された誘導起電力もまた、後続の静的構造解析で利用することができます。
in an electric junction
Maxwellの方程式から導出される解を様々な問題に対して適用することができます。:
- ・ 渦電流
- ・ 誘導問題
- ・ 共振空洞
- ・ 波動伝播
- ・ 一般的な動電場問題
PEMRMASで定義できるすべての種類の荷重を動的解析に適用することができます(強制電位など)。この定義は、静的荷重ケースと適切な時間関数との組み合わせで指定することができ、 動的応答解析における動的荷重の定義と同様です。
model and magnetic field strength (top), induced heat
flux and plastic strains (below).
